the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Earth's surface mass transport derived from GRACE, evaluated by GPS, ICESat, hydrological modeling and altimetry satellite orbits
Christian Gruber
Sergei Rudenko
Andreas Groh
Dimitrios Ampatzidis
Elisa Fagiolini
The Gravity Recovery and Climate Experiment (GRACE) delivered the most accurate quantification of global mass variations with monthly temporal resolution on large spatial scales. Future gravity missions will take advantage of improved measurement technologies, such as enhanced orbit configurations and tracking systems, as well as reduced temporal aliasing errors. In order to achieve the latter, sub-monthly to daily innovative models are computed. In addition, non-conventional methods based on radial basis functions (RBFs) and mascons will give the ability to compute models in regional and global representations as well. We show that the RBF modeling technique can be used for processing GRACE data yielding global gravity field models which fit independent reference values at the same level as commonly accepted global geopotential models based on spherical harmonics.
The present study compares for the first time a complete global series of solutions in order to quantify recent ice mass changes. We further compare the ice-induced crustal deformations due to the dynamic loading of the crustal layer with the Global Positioning System (GPS) uplift measurements along Greenland's coastline. Available mass change estimates based on Ice, Cloud, and land Elevation Satellite (ICESat) laser altimetry measurements both in Greenland and Antarctica are used to assess the GRACE results.
A comparison of GRACE time series with hydrological modeling for various basin extensions reveals overall high correlation to surface and groundwater storage compartments. The forward computation of satellite orbits for altimetry satellites such as Envisat, Jason-1 and Jason-2 compares the performance of GRACE time-variable gravity fields with models including time variability, such as EIGEN-6S4.
- Article
(6424 KB) - Full-text XML
- BibTeX
- EndNote
Until 2017, the Gravity Recovery And Climate Experiment (GRACE; Tapley et al., 2004) had measured temporal variations of Earth's gravitational field highly accurately to only a few tens of µGal. These data provide valuable information on the distribution and variation of mass in the Earth's subsystems such as the atmosphere, hydrosphere, ocean and cryosphere. The GRACE time series of monthly gravity field solutions are computed in terms of spherical harmonic model coefficients at the German Research Centre for Geosciences (GFZ), version RL05a, University of Texas/Center for Space Research (CSR), version 05 and Technical University Graz, Institute of Geodesy (ITSG), version 2016, each of which shows significantly less noise and spurious artifacts compared to their predecessors.
The Earth observation missions GRACE and GRACE Follow-On provide the only way to estimate groundwater storage changes on a global scale and in remote areas. Moreover, and in order to gain further knowledge on mass transport of short appearances, regional solutions in areas of strong anomalous signals have been developed and new methods for their computation can be investigated. A candidate approach in this aspect is the transformation of the measurement data to in situ (proxy) gravity observables with subsequent inversion and continuation by means of rigorous integral equations. This non-conventional approach for the analysis of GRACE inter-satellite range observations, processed in combination with best knowledge reduced dynamic GRACE orbits has been elaborated in Gruber et al. (2014) and a detailed theoretical foundation of the method is presented in Gruber et al. (2018). In brief, the transformed observations are first reduced by available geophysical background models and subsequently inverted as well as continued downward by a rigorous formulation in terms of reproducing kernel functions. Then, time-variable mass equivalent anomaly maps with respect to the subtracted background data are derived.
The observation equations are solved in spatial representation and are well suited for Kalman-filtered solutions, as covariance information is not required in spectral domain and can be applied to regional and insular domains only. This gives the opportunity to enhance the temporal resolution towards sub-monthly (weekly or daily) time series and to advance into local domains, thereby preserving the accuracy that is achieved from the standard monthly inversions.
In the present article, we discuss the following evaluation methods with our latest results:
- i.
continental uplift rates from the Greenland Global Positioning System (GPS) network (G-NET) and Center for Orbit Determination in Europe (CODE);
- ii.
ice mass balances from the Ice, Cloud, and land Elevation Satellite (ICESat);
- iii.
hydrological basin comparison against the WaterGAP hydrological model (WGHM); and
- iv.
altimetry satellite orbits: satellite laser ranging (SLR) and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) observation fits and arc overlaps.
In the present approach, residual daily mass equivalents of the atmosphere, non-steric ocean topography and gravity changes within the hydrological storage system are estimated in a Kalman filter approach from the observed acceleration differences between the GRACE twin satellites, known as acceleration approach, e.g., Rummel (1979). Here, we make use of a formulation by integral equations and an explicit Kernel function, given by Novák (2007). The Kalman filter, first applied to GRACE data by Kurtenbach et al. (2009, 2012), is used by us to transform the GRACE gradient-like observation data. The main features are a stochastic process model for the data prediction step and the conversion of the range measurements to in situ gravity observations. Standard integral equations solve for the surface mass equivalents that are concentrated on a thin layer at the surface of a spherical Earth (Wahr et al., 1998). The applied Poisson kernel function thereby isotropically localizes the signal in spatial domain in contrast to a localization in spectral domain where global multi-pole moments (spherical harmonic coefficients) are estimated.
During least-squares prediction, the surface grid tiles for the following day are recursively computed from the previous day and consecutively updated by the L1B observations in the Kalman gain. Despite the large number of observation samples (every 5 s), the problem remains in practice ill-posed, due to an incomplete data coverage of the Earth's sphere in space and time (ground track coverage and variation) and ambiguous signal continuation from orbital altitude downward to Earth's mean radius.
Therefore, it is useful to stabilize results using available geophysical background information for the expected signals and model their stochastic behavior as an additional momentum. This can be done by using signal and error covariances in the time-varying storage systems, as well as the noise characteristics of the (residual) observables from the remote sensor system. The latter noise type mainly stems from the ranging and accelerometer instruments, the orbital trajectory determination and the subtracted background model uncertainty. The improperly posed inverse problem is then constrained in two aspects.
Firstly, it is constrained by the applied background modeling that has been derived from available monthly GRACE solutions and trends, as well as annual signal estimates thereof. Secondly, it is constrained by the stochastic modeling of additional atmospheric and hydrological signal variations derived from geophysical models. These are the short-term atmospheric and non-tidal ocean mass variations, regularly published alongside the monthly gravity field products, stemming from external data sources such as surface pressure records from the European Centre for Medium-Range Weather Forecasts (ECMWF) and the Ocean Model for Circulation and Tides (OMCT) (Dobslaw et al., 2013). They are provided in an external operational product, AOD1B, and are the strongest aliasing signal due to their high variability that is below the feasible GRACE temporal solution. In the current processing, 6-hourly files were removed from the GRACE gradient differences beforehand and were averaged into daily products used for the empirical auto- and cross-covariance estimates. We propagate their characteristics as background model deficiency, approximated by one-third of the AOD1B signal, through the Kalman filter, i.e., process error prediction and transition. Further, the WaterGAP hydrological model (WGHM; Döll et al., 2003) was used to derive the signal covariances for continental hydrology.
It is then not necessary to post-filter the results, as they do not exhibit typical anisotropic artifacts from the subsequent data inversion. The formal accuracy estimates are found in the updated Kalman covariances that are co-estimated epoch-wise with the states. This results in an equivalent accuracy as obtained from a regularized solution and is based on error propagation during the time update and a least-squares prediction error. For further details, the reader is referred to Gruber et al. (2018). For more general reading on improperly posed inverse problems, refer to Marchenko (2009).
Despite the regularized processing methodology, the system is very capable of capturing hydrogeophysical signals in their respective amplitudes. Some of the key advantages of the presented method can be summarized as follows:
-
enhanced temporal resolution, reduced aliasing and artifacts;
-
regional solution and refinement, if local covariance information is available;
-
no required post-filtering (user friendly);
-
spatial constraining (e.g., land–ocean decoupling);
-
linear equations and low computational cost; and
-
mutual combination with other space gravimetric techniques, such as satellite laser ranging, gradiometry and sea surface topography from altimetry.

Figure 1Correlations between the G-NET station uplift and the ice-induced crustal deformations due to dynamic loading of the crustal layer obtained using the temporal gravity field solutions. Only very minor differences for GFZ RBF and CSR RL05, mainly in the eastern part of Greenland, can be exhibited.
A significant spread of ice mass loss into northwest Greenland has been observed by GRACE and GPS during recent years (see Khan et al., 2010). We make use of monthly averaged vertical GPS site displacements from G-NET, led by Ohio State University's division of Geodetic Science. G-NET is a network of 46 continuous GPS stations, installed on bedrock, spread across Greenland. We compare them with the crustal deformations inferred from post-filtered monthly GRACE gravity fields of ITSG-Grace2016 (Mayer-Gürr et al., 2016), GFZ Release 5a (Dahle et al., 2012), CSR Release 5 (Bettadpur et al., 2012) and the monthly averaged solutions derived from spherical radial basis functions (GFZ RBF). It should be noted that GPS site data are point values, whereas the GRACE solutions stem from area integrals. While this does not exclude direct comparison between the two data sets, insular discrepancies can be expected.
The simultaneous use of GNSS and GRACE data is a subject that has already been discussed in detail in the geodetic literature, e.g., Kusche and Schrama (2005) and van Dam et al. (2007). The aforementioned publications focus on the comparison between the GPS and GRACE products, in terms of the regional or global mass distribution and/or the vertical displacements, respectively.
We firstly complete all models with a center-of-mass to a center-of-figure translation by degree 1, following Swenson et al. (2008). Changes in the ocean mass cause an offset between the center-of-mass and the center-of-figure frame, commonly denoted as geocenter motion. Briefly, any natural and anthropogenic water mass redistribution at Earth's surface causes changes in global ocean mass. Net inflow of fresh water and exchange between ice and water are typical phenomena that affect eustatic sea level variability. The changes are reflected in the geocenter motion (degree 1) and are non-negligible for the GRACE mission. Since the global eustatic sea level variations are excluded from the de-aliasing model, they can be derived empirically from the gravity field solutions.
Secondly, the Earth's flattening (C2,0) being poorly observed by GRACE is replaced by a SLR-derived time series from Cheng et al. (2013) in the spherical harmonic models (ITSG-Grace2016, GFZ RL05a, CSR RL05). The flattening variations in the case of the GFZ RBF solutions remain unchanged after their co-estimation during Kalman filtering.
The atmospheric and non-tidal ocean loading (GAC) is added back to the GRACE-inferred mass changes, and the glacial isostatic adjustment (GIA) is removed from the temporal GRACE coefficients using the GIA predictions according to the ICE-5G v1.3 model (Peltier, 2004). This step is required to avoid propagation of gravity changes that are caused by the vertical displacements from GIA into the lithosphere uplift calculation from GRACE, which should reflect only the viscoelastic part. The corresponding forward computation for the G-NET sites is then obtained by means of the viscoelastic load Love numbers ( and ) according to Farrell (1972).
Finally, the named GIA-induced uplift from the ICE-5G v1.3 model is again restored, whereby the buoyancy effect at the base of the lithosphere (Wahr, 1995) is taken into account. At each site, the vertical displacements from the GPS time series are then correlated with the GRACE results (from monthly means) and computed over all stations.
Figure 1 shows the correlations between the G-NET station uplift and the ice-induced crustal deformations due to dynamic loading of the crustal layer obtained using the temporal gravity field solutions: GFZ RBF and CSR RL05. The relatively lower correlations with G-NET around the eastern stations at 74∘ N (dane, hmbg, wthg) can be explained by deficiencies in the GIA uplift model (Ingo Sasgen, personal communication, July 2017), which was therefore left out for the computation of the average correlation numbers. These average correlations over the stations are very high, with some minor, insignificant deviations: GFZ RL05a: 90.2 %, ITSG-Grace2016: 90.1 %, CSR RL05: 89.6 % and GFZ RBF: 89.0 % .

Figure 2Correlations of the vertical station variations inferred from GFZ GRACE RBF solutions and the global GPS station network from CODE. Only stations with correlations r>0.2 (in total 95 stations) are considered.
Then, the global GPS station network displacements from the Center for Orbit Determination in Europe (CODE), computed by Steigenberger et al. (2011) for the time span of 2002–2012, are treated accordingly. In Fig. 2, the correlations of the vertical station variations inferred from GFZ GRACE RBF solutions and selected CODE GPS stations are displayed. Due to minor differences between the individual solutions, the GFZ RBF solutions are displayed and serve as proxy for GFZ RL05a, ITSG-Grace2016 and CSR RL05 as well. Average correlations for the stations with correlations r greater than 0.2 (in total 95 stations) are CSR RL05: 56.8 %, GFZ RBF: 56.6 %, GFZ RL05a: 53.9 % and ITSG-Grace2016: 53.5 %. The reason why the global station network generally correlates less than the G-NET sites can be explained by the uplift signal strength and the individual data quality (disruptions or damages) but also by their location, e.g., on islands or coastal regions where signal separation is difficult. One should keep in mind that we are comparing (post-filtered) area mean values from GRACE with point values from GPS such that aliasing of neighboring signal occurs. Nevertheless, for many stations, the correlations are high (blue dots) and strongly support the ability of GRACE to remotely monitor mass-induced uplift rates.
The extent of the Arctic sea ice reached a new record low in September 2012. According to the European Environment Agency (2016), climate change causes sea ice melting in the region at a rate much faster than estimated by earlier projections. The snow cover also shows a downward trend. The melting Arctic might impact the people not only living in the region but also elsewhere in Europe and beyond.
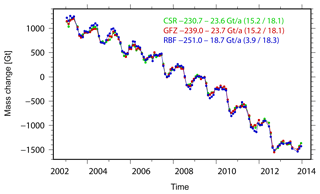
Figure 3Greenland linear ice sheet mass change estimates per year from different GRACE solutions (CSR RL05, GFZ RL05a and GFZ RBF) from January 2003 to December 2013. Values in brackets indicate different components of the total error budget (GIA model uncertainties – last value; all remaining error contributions, including leakage errors and GRACE errors – first value).
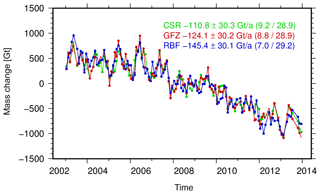
Figure 4Antarctic linear ice sheet mass change estimates per year from different GRACE solutions (CSR RL05, GFZ RL05a and GFZ RBF) from January 2003 to December 2013. Values in brackets indicate different components of the total error budget (GIA model uncertainties – last value; all remaining error contributions, including leakage errors and GRACE errors – first value).
Ice mass changes of both the Greenland Ice Sheet (GIS) and the Antarctic Ice Sheet (AIS) are inferred from monthly gravity fields of different GRACE solutions (GFZ RL05a, CSR RL05 and GFZ RBF). Except for GFZ RBF, all solutions are filtered using an anisotropic decorrelating filter (DDK4; Kusche et al., 2009). Spherical harmonic degree 1 coefficients are added as described in Sect. 3, along with the Earth's oblateness, C2,0. Mass changes of the solid Earth due to GIA are corrected by means of the ICE-5G v1.3 model for the GIS and the IJ05_R2 model (Ivins et al., 2013) for the AIS. All results presented in the following are updates of the findings in Groh et al. (2014a, b) to which the reader is referred for a detailed description of the processing.
Mass change time series for the GIS (January 2003–December 2013) are shown in Fig. 3. All time series are in good agreement and exhibit comparable linear and seasonal variations. Only minor differences are visible for specific periods. In general, the mass change time series for the AIS (Fig. 4) are also in good agreement. Although differences in the linear trend estimates are visible, they still agree with the corresponding accuracy measures, which are clearly dominated by remaining uncertainties in the GIA predictions.
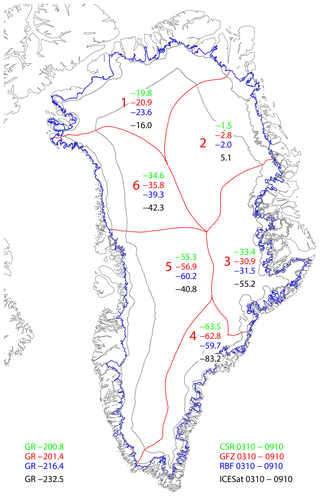
Figure 5Mean annual ice mass change (Gt a−1) for the Greenland Ice Sheet and selected drainage basins (separated by red lines) and aggregations derived from different GRACE solutions and ICESat laser altimetry data over the period from October 2003 to October 2009.
ICESat laser altimetry observations can be used to derive linear ice mass changes over Greenland and Antarctica, which can be compared to corresponding GRACE results. Here, we utilize the ICESat-derived mass change estimates presented in Groh et al. (2014a, b) to compare them to our GRACE ice mass trend estimates for the period October 2003–October 2009, the operational period of ICESat. Additional trend estimates for selected drainage basins are compared in Fig. 5. Despite the different observation techniques and resolution capabilities, Fig. 5 reveals the overall agreement between the tested solutions. Still, some differences between the ICESat results and the three GRACE solutions exist. For example, the ICESat results for eastern Greenland exceed those from GRACE substantially. Moreover, while GRACE observes a mass gain for the East Antarctic Ice Sheet, the opposite conclusion can be drawn from the ICESat results. These differences can be related to the different error sources of both techniques. Moreover, limitations in the density assumption (here density of pure ice) used to convert altimetric height changes into mass change can also contribute to the revealed differences.
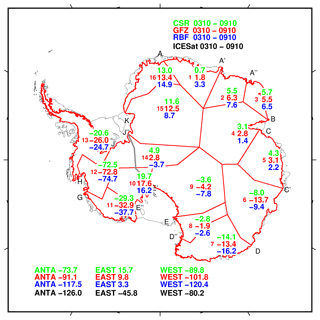
Figure 6Mean annual ice mass change (Gt a−1) for both the Antarctic Ice Sheet and selected drainage basins (separated by red lines) and aggregations derived from different GRACE solutions and ICESat laser altimetry data over the period from October 2003 to October 2009. The grey line depicts the boundary between the eastern and western parts of the AIS.
Global catchment aggregated values (CAVs) for hydrological basins greater than ≈50 000 km2 are computed from WGHM (Döll et al., 2003) and compared to the equivalent water layer variations (EWHs, according to Wahr et al., 1998) from results obtained from GRACE. The aggregation is performed by equally weighted sums over regular surface tiles. The GRACE monthly fields are used after post-processing with DDK4 according to Kusche et al. (2009), consistently for the spherical harmonic models (CSR RL05, GFZ RL05a and ITSG-Grace2016) and monthly mean values of daily Kalman-filtered results for the GFZ RBF solution. The GRACE data are again reduced for GIA and seasonal variations are removed beforehand from all data sets in order to focus on non-seasonal coherence. Moreover, in the case of the GFZ RBF solution, the seasonal cycle has already been introduced as a time-variable background model.
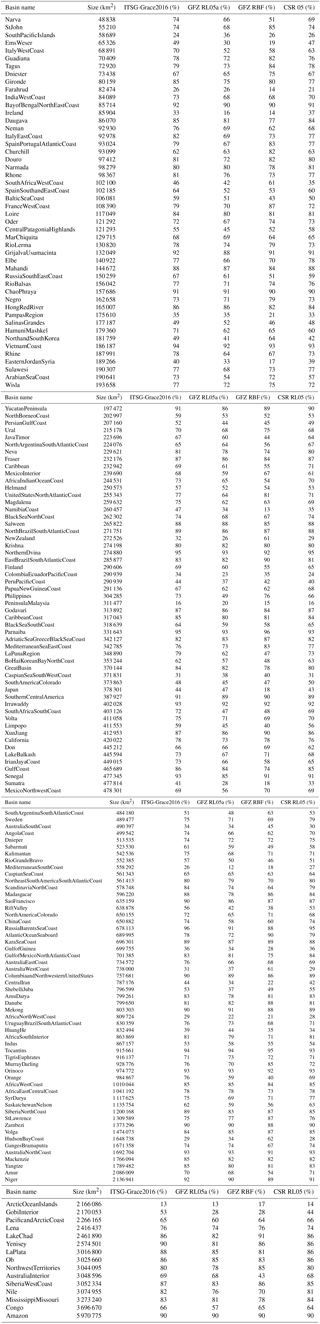
The database containing in total 188 basins (of which 163 are used) was obtained from the interactive GeoNetwork (FAO, 2015). We use (i) Pearson's bivariate correlation coefficient (XO), (ii) the standard deviation (SD) of the differences between two series and (iii) the scale corresponding to the GRACE basin series with respect to its hydrological counterpart, in order to reveal their agreement. The averaged agreement is displayed in Table 1. A positive correlation threshold of 10 % is presumed for the individual GRACE solutions for each basin to exclude (e.g., deserts or islands), where a strong impact from signal leakage of surrounding water deteriorates our results. All four solutions perform very similarly, with only minor differences mainly discovered in terms of correlations to the hydrological model (WGHM) over the time span of 2002–2013. While the correlation gives an opportunity to determine how coherent our remotely sensed results represent a certain “ground truth”, the standard deviation (SD) of the differences indicates the reliability of the results. The amplitudes indicate to which extent remote mass balances are captured on average.
The best correlation results are found for the ITSG-Grace2016 solution, with 60.5 % for the de-seasoned results and 70.6 % for the full signal. The lowest standard deviations of the differences to hydrological basin averages are found with 4.4 cm for GFZ RBF after de-seasoning and 7.4 cm for the full signal. The best scale correspondence which projects GRACE basin estimates onto the reference hydrology is found for the GFZ RBF solutions. GRACE-equivalent water layer estimates thus capture, on average, most of the hydrological signal strength.
Table 1Comparison of the average GRACE basin estimates against hydrological modeling (WGHM). Bold-faced numbers highlight the best performance in the category. Values in brackets are obtained if the seasonal signal is included. “SD” indicates standard deviation.

Figure 7 displays the comparative correlations for each basin with respect to the hydrological model (WGHM) which represents total water storage variations throughout the period 2002–2013. This comparison provides a performance indicator for different GRACE solutions by means of their individual agreement with WGHM on the level of CAVs and geographical location.
Still, it remains difficult to identify systematic patterns such as basin size or basin location that would indicate, e.g., data sampling or specific processing properties. The results overall strongly support the capability of GRACE to monitor global water storage variations remotely from space despite the band limitation of the solutions and their signal omission errors.
To counteract this, in Steckler et al. (2010), the basin-scale masks for water loading in Bangladesh were processed by a truncated spherical harmonic representation in order to simulate the omission error from the model resolution. In our approach, we have converted each fine-scale basin mask of into a coarse mask of , which entirely includes the fine-scale mask in the sense of a convex hull. The domain is thus enlarged to encounter to a certain extent for signal leakage-out effects. On the other hand, leakage-in effects cannot be treated effectively other than by an increased model resolution under the provision that the measurement system is sensitive to it. The main limitations thus remain gravity signal attenuation at GRACE mission altitude and the separation width of the twin satellite system.
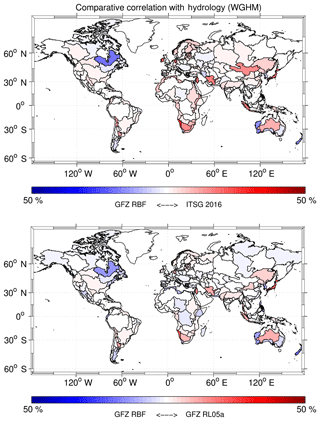
Figure 7Comparative correlations of catchment aggregated values from GRACE results against hydrology; the plot depicts the relative difference (%) in each basin between the correlations of two time series with respect to the hydrological model (WGHM). Blue indicates higher coherence for the GFZ RBF solution and red marks higher coherence for the concurring model (GFZ RL05a, ITSG-Grace2016). HudsonBayCoast and Japan stick out slightly, which hints at post-glacial rebound and the Tohoku megathrust earthquake; see also the text for further discussion. For a full list of all considered basins and their individual hydrological correlations, the reader is referred to Table A1 in the Appendix.
Recently, the impact of time-variable geopotential models on altimetry satellite orbits has been investigated (Rudenko et al., 2014). Following these ideas, we test the GFZ RBF solutions for precise orbit determination of Envisat (2002–2012), Jason-1 (2002–2013) and Jason-2 (2008–2015) at the time intervals given in the parentheses. We have chosen these satellites since their missions coincide with the GRACE time interval. The orbits are derived at 7-day arcs for Envisat and 12-day arcs for Jason-1 and Jason-2 by using the same background models for each satellite (Rudenko et al., 2017) but choosing three different Earth gravity field models/solutions: EIGEN-6S4 (Förste et al., 2016), GFZ RBF and GFZ RL05a. For the propagation of the orbits based on the GFZ RBF time-variable part, we first convert the grid tiles into spherical harmonic coefficients and add the static part of the EIGEN-6S4 model. The static part of the satellite-only global gravity field model EIGEN-6S4 is complete up to degree and order 300. The time-variable gravity part of the model is represented by a drift, and annual and semi-annual variations per year of spherical harmonic coefficients up to degree and order 80 by 1 July 2014.
We have computed fits (observed minus calculated) of SLR and DORIS observations used for precise orbit determination of the satellites and 2-day arc overlaps. Since the only difference in our tests consists of a replacement of Earth's gravity field models/solutions, smaller values of observation fits and arc overlaps indicate better performance of a respective Earth gravity field model/solution. The mean values of SLR and DORIS rms fits and 2-day radial arc overlaps for each satellite obtained using the EIGEN-6S4 model, GFZ RL05a and GFZ RBF solutions are shown in Table 2.
Table 2The mean values of SLR and DORIS rms fits and 2-day radial arc overlaps for Envisat (2002–2012), Jason-1 (2002–2013) and Jason-2 (2008–2015), obtained using the EIGEN-6S4 model, GFZ RBF and GFZ RL05a solutions.
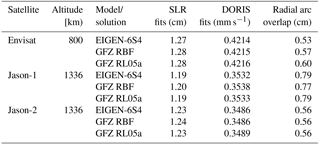
The results obtained using the GFZ RBF solutions are in agreement with those obtained using the EIGEN-6S4 model and slightly outperform the results obtained using the GFZ RL05a solution. Since Envisat is more sensitive to the Earth's gravitational field due to its lower altitude than the two Jason satellites, we look at the results obtained for this satellite in more detail. The DORIS measurements (Fig. 8) seem to be less suitable to detect the impact of the replacement of the EIGEN-6S4 gravity field model by GFZ RBF solutions, since there are no notable differences in the fits of these observations derived from different Earth gravity field realizations.
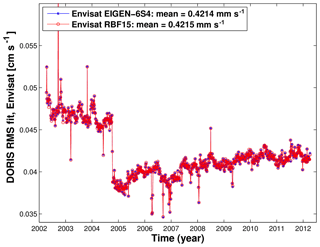
Figure 8Weekly DORIS rms fits of Envisat computed with different time-variable Earth gravity modeling: EIGEN-6S4 model and GFZ RBF solution.
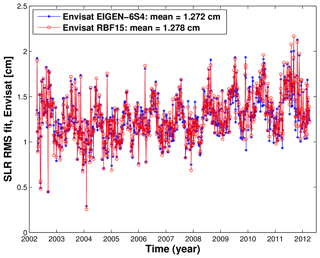
Figure 9Weekly SLR rms fits of Envisat computed with different time-variable Earth gravity modeling: EIGEN-6S4 model and GFZ RBF solution.
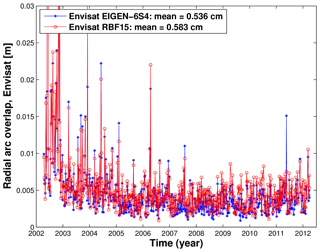
Figure 10Weekly 2-day radial arc overlaps for Envisat computed with different time-variable Earth gravity modeling: EIGEN-6S4 model and GFZ RBF solution.
SLR rms fits (Fig. 9) show comparable or even better performance (smaller rms fits) at some orbital arcs for Envisat until the middle of 2008, when using GFZ RBF solutions, and better performance when using the EIGEN-6S4 model from the middle of 2008 onwards. This is probably caused by insufficient gravity field trend estimates in the background modeling and can be addressed in the next iteration. The inconsistency is also confirmed when looking at weekly obtained 2-day arc overlaps in Fig. 10. The radial arc overlaps are of comparable accuracy when using GFZ RBF, GFZ RL05a solutions and the EIGEN-6S4 model for Jason-1 and Jason-2, while for Jason-1, the GFZ RBF solutions even outperform the model and other solutions; see Table 1.
We show in this study that the RBF processing technique can be used for processing GRACE data yielding global gravity field models which fit independent reference values at the same level as commonly accepted global geopotential models based on spherical harmonics. In this study, a set of evaluation methods is used to compare the novel RBF GRACE solutions with other widely used standard GRACE solutions. The results of our evaluation confirm once again the high potential and ability of GRACE or GRACE-like missions to significantly contribute to climate-relevant indicators such as the quantification of ice mass loss over Greenland. While a single correlation result gives only limited evidence of the overall quality of a solution, the sum over several evaluations may provide a fair picture of the relative performance in a close comparison with each other. The obtained spread of results is found relatively small and has clearly converged with each new release; however, still minor differences are found and may help to further improve the data processing methods within the GRACE community.
More in detail, the comparison to the G-NET and CODE GPS uplift rates confirms the temporal loading of mass redistribution that is revealed in the GRACE solutions. Both vertical data sets have helped in the past to validate and confirm the spatial resolution of the GRACE results. All four GRACE time-variable gravity field solutions that we have tested (ITSG-Grace2016, GFZ RL05a, GFZ RBF and CSR RL05) show consistently high correlations (89 %–90 %) with the vertical site displacements from the G-NET GPS network. The correlations to the global GPS station network from CODE are lower (52 %–55 %). This can be explained by the lower uplift signal strength and the individual data quality but also due to their location, e.g., on islands. However, for many stations, the correlations are high and confirm the ability of GRACE to remotely monitor mass-induced uplift rates.
Our direct comparison of linear ice mass changes from the ICESat results with the GRACE loading data reveals very good agreement, but also spatial differences, when comparing over smaller drainage basins.
The comparative agreement with the hydrological model (WGHM) shows that monthly means of the GFZ RBF solutions are of equal quality to the renowned products. All GRACE models under consideration perform very similarly and support the fact that large-scale hydrology can be accurately monitored remotely from space, especially the trend estimates of the Earth's polar ice sheets melting and groundwater depletion over large deserted areas. The transformation of the K-band and trajectory data from dynamic to in situ observations has been successfully used to compute the GFZ RBF solutions. An improved de-aliasing for monthly gravity field products is feasible when estimating additional sub-monthly results for time-variable gravity signals and residual atmosphere and oceanic loading. The (Kalman) regularization reduces artifacts during inversion so that no post-filtering is indicated for these products.
Precise orbit determination of low-orbit Earth's satellites, e.g., Envisat, has been shown to be a powerful tool to validate daily and monthly Earth time-variable gravity field solutions. In general, the orbit tests for altimetry satellites Envisat, Jason-1 and Jason-2 over the total 2002–2015 time interval show rather comparable quality to the orbits derived using the EIGEN-6S4 model, GFZ RBF and GFZ RL05a solutions. DORIS measurements seem to be less sensitive to the replacement of up-to-date time-variable Earth gravity field models and solutions. On the contrary, SLR residuals and arc overlaps of altimetry satellite orbits are sensitive to the quality of the underlying background models. From 2002 to the middle of 2008, SLR rms fits of Envisat obtained using GFZ RBF solutions perform comparably and even better in some weeks than those derived using the EIGEN-6S4 model, whereas this model outperforms the GFZ RBF solutions from 2008 onwards. Radial arc overlaps are of comparable accuracy when using GFZ RBF, GFZ RL05a solutions and the EIGEN-6S4 model for Jason-1 and Jason-2, while for Jason-1, the GFZ RBF solutions even outperform the model and other solutions. For Envisat, which is more sensitive to the gravity field modeling, the smallest radial arc overlaps are obtained using the EIGEN-6S4 model, followed by GFZ RBF solutions and finally by GFZ RL05a solutions. In this context, future reprocessing of GRACE time series can be verified against altimetry results to confirm further improvements. In view of the GRACE Follow-On mission with improved instrument data, we may expect time-variable gravity fields to be included in future orbit computations of altimetry satellites.
Latest daily grids in equivalent water heights and grids with GIA predictions removed and center of mass to center of figure corrected, as well as spherical harmonic coefficients, can be downloaded from ftp://ftp://gfzop.gfz-potsdam.de/EGSIEM/ (last access: 2 December 2018).
For details about the maximum resolution, error estimates and low-degree harmonic coefficients, the interested reader is referred to the corresponding file (ftp://gfzop.gfz-potsdam.de/EGSIEM/readme; last access: 2 December 2018).
Table A1List of global hydrological catchment basins sorted by area. The correlations refer to the signal from GRACE-derived water storage variations and the hydrological model (WGHM) after de-seasoning. The given numbers are a performance indicator for the individual solutions in a relative context.
CG derived the daily gravity field maps and has led the research. SR was committed to the orbit computation and cross-comparison with altimetry satellite orbits. AG provided the ICESat results and consistent comparisons with GRACE data over the glacial regions, DA took care of the GPS vertical site displacements, and EF was responsible for the atmosphere and ocean de-aliasing products.
The authors declare that they have no conflict of interest.
We would like to thank the German Space Operations Center (GSOC) of the German Aerospace Center (DLR) for providing continuous and nearly 100 % of the raw telemetry data of the twin GRACE satellites. The WGHM hydrological data sets are greatly appreciated. We would like also to thank the CODE processing team for providing the CODE data, and the Greenland GPS station network for providing the G-NET vertical displacements. Ryan L. Sink is thanked for English lecturing. We also thank the editor and two referees for their comments that allowed us to improve this article.
This research was partly supported by the European Space Agency (ESA) within
the Climate Change Initiative Sea Level phase 2 project and by the German
Research Foundation (DFG) within the project “Consistent dynamic satellite
reference frames and terrestrial geodetic datum parameters”. SLR and DORIS
data available from the International Laser Ranging Service (ILRS) and
International DORIS Service (IDS) were used in this research. One of the
authors (Christian Gruber) was funded by the European Union's Horizon 2020
project European Gravity Service for Improved Emergency Management (EGSIEM)
under grant agreement no. 637010. This article reflects only the authors'
views. The Research Executive Agencies are not responsible for any use that
may be made of the information it contains.
The article processing charges for this open-access
publication were covered by a Research
Centre of the
Helmholtz Association.
Edited by: David
Lundbek Egholm
Reviewed by: two anonymous referees
Bettadpur, S. and CSR Level-2 Team: Insights into the Earth System mass variability from CSR-RL05 GRACE gravity fields, EGU General Assembly, Vienna, Austria, 22–27 April 2012, EGU2012-6409, 2012.
Cheng, M., Tapley, B. D., and Ries, J. C.: Deceleration in the Earth's oblateness, J. Geophys. Res.-Sol. Ea., 118, 740–747, https://doi.org/10.1002/jgrb.50058, 2013.
Dahle, Ch., Flechtner, F., Gruber, Ch., König, D., König, R., Michalak, G., and Neumayer, K.-H.: GFZ GRACE Level-2 Processing Standards Document for Level-2 Product Release 0005, Scientific Technical Report STR12/02 – Data, Revised Edition, January 2013, Potsdam, 21 pp., https://doi.org/10.2312/GFZ.b103-1202-25, 2012.
Dobslaw, H., Flechtner, F., Bergmann-Wolf, I., Dahle, C., Dill, R., Esselborn, S., Sasgen, I., and Thomas, M.: Simulating high-frequency atmosphere-ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL05, J. Geophys. Res., 118, 3704–3711, 2013.
Döll, P., Kaspar, F., and Lehner, B.: A global hydrological model for deriving water availability indicators: model tuning and validation, J. Hydrol., 270, 105–134, 2003.
European Environment Agency (EEA): The melting Arctic, http://www.eea.europa.eu/articles/the-melting-arctic/#parent-fieldname-title (last access: 2 December 2018), 2012.
Farrell, W.: Deformation of the Earth by Surface Loads, Rev. Geophys., 10, 761–797, https://doi.org/10.1029/RG010i003p00761, 1972.
Förste, C., Bruinsma, S.L., Rudenko, S., Abrikosov, O., Lemoine, J.-M., Marty, J.-C., Neumayer, K. H., and Biancale, R.: EIGEN-6S4 A time-variable satellite-only gravity field model to d/o 300 based on LAGEOS, GRACE and GOCE data from the collaboration of GFZ Potsdam and GRGS Toulouse, GFZ Data Services, https://doi.org/10.5880/icgem.2016.004, 2016.
GeoNetwork, Food and Agriculture Organization of the United Nations (FAO): http://www.fao.org/geonetwork/srv/en/main.home (last access: 2 December 2018), 2015.
Groh, A., Ewert, H., Fritsche, M., Rülke, A., Rosenau, R., Scheinert, M., and Dietrich, R.: Assessing the current evolution of the Greenland Ice Sheet by means of satellite and ground-based observations, Surv. Geophys., 35, 1459–1480, https://doi.org/10.1007/s10712-014-9287-x, 2014a.
Groh, A., Ewert, H., Rosenau, R., Fagiolini, E., Gruber, Ch., Floricioiu, D., Abdel Jaber, W., Linow, S., Flechtner, F., Eineder, M., Dierking, W., and Dietrich, R.: Mass, volume and velocity of the Antarctic Ice Sheet: present-day changes and error effects, Surv. Geophys., 35, 1481–1505, https://doi.org/10.1007/s10712-014-9286-y, 2014b.
Gruber, Ch. and Gouweleeuw, B.: Short latency monitoring of residual continental, ocean and atmosphere mass variations using GRACE inter-satellite accelerations, Geophys. J. Int., in review, 2018
Ivins, E., James, T., Wahr, J., Schrama, E., Landerer, F., and Simon, K.: Antarctic contribution to sea level rise observed by GRACE with improved GIA correction, J. Geophys. Res.-Sol. Ea., 118, 3126–3141, https://doi.org/10.1002/jgrb.50208, 2013.
Gruber, Ch., Moon, Y., Flechtner, F., Dahle, Ch., Novák, P., König, R., and Neumayer, K.-H.: Submonthly GRACE solutions from localizing integral equations and Kalman filtering, Earth on the Edge: Science for a Sustainable Planet, Proceedings of the IAG General Assembly, Melbourne, Australia, 28 June–2 July 2011, Series: International Association of Geodesy Symposia, edited by: Rizos, W., 139, 383–389, ISBN 978-3-642-37222-3, 2014.
Khan, S. A., Wahr, J., Bevis, M., Velicogna, I., and Kendrick, E.: Spread of ice mass loss into northwest Greenland observed by GRACE and GPS, Geophys. Res. Lett., 37, L06501, https://doi.org/10.1029/2010GL042460, 2010.
Kurtenbach, E., Mayer-Gürr, T., and Eicker, A.: Deriving daily snapshots of the Earth gravity field from GRACE L1B data using Kalman filtering, Geophys. Res. Lett., 36, L17102, https://doi.org/10.1029/2009GL039564, 2009.
Kurtenbach, E., Eicker, A., Mayer-Gürr, T., Holschneider, M., Hayn, M., Fuhrmann, M., and Kusche, J.: Improved daily GRACE gravity field solutions using a Kalman smoother, J. Geodyn., 59–60, 39–48, 2012.
Kusche, J. and Schrama, E. J. O.: Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data, J. Geophys. Res., 110, B09409, https://doi.org/10.1029/2004JB003556, 2005.
Kusche, J., Schmidt, R., Petrovic, S., and Rietbroek, R.: Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model, J. Geod., 83, 903–913, https://doi.org/10.1007/s00190-009-0308-3, 2009.
Marchenko, A. N.: On the Global Density Distribution Based on the Earths Mechanical Parameters and Piecewise Reference Model, in: Mission and Passion: Science A volume dedicated to Milan Bursa on the occasion of his 80th birthday, edited by: Holota, P., Czech National Committee of Geodesy and Geophysics, Prague, 169–179, 2009.
Mayer-Gürr, T., Behzadpour, S., Ellmer, M., Kvas, A., Klinger, B., and Zehentner, N.: ITSG-Grace2016 – Monthly and Daily Gravity Field Solutions from GRACE, GFZ Data Services, https://doi.org/10.5880/icgem.2016.007, 2016.
Novák, P.: Integral Inversion Of SST Data Of Type GRACE, Stud. Geophys. Geod., 51, 351–367, 2007.
Peltier, W. R.: Global Glacial Isostasy and the Surface of the Ice-Age Earth: The ICE-5G (VM2) Model and GRACE, Ann. Rev. Earth Pl. Sc., 32, 111–149, 2004.
Rudenko, S., Dettmering, D., Esselborn, S., Schöne, T., Förste, Ch., Lemoine, J.-M., Ablain, M., Alexandre, D., and Neumayer, K.-H.: Influence of time variable geopotential models on precise orbits of altimetry satellites, global and regional mean sea level trends, Adv. Space Res., 54, 92–118, https://doi.org/10.1016/j.asr.2014.03.010, 2014.
Rudenko, S., Neumayer, K.-H., Dettmering, D., Esselborn, S., Schöne, T., and Raimondo, J.-C.: Improvements in precise orbits of altimetry satellites and their impact on mean sea level monitoring, IEEE T. Geosci. Remote, 55, 3382–3395, https://doi.org/10.1109/TGRS.2017.2670061, 2017.
Rummel, R.: Determination of short-wavelength components of the gravity field from satellite-to-satellite tracking or satellite gradiometry an attempt to an identification of problem areas, Man. Geodyn., 4, 107–148, 1979.
Steckler, M. S. Nooner, S. L. Akhter, S. H., Chowdhury, S. K., Bettadpur, S., Seeber L., and Kogan, M.: Modelling Earth deformation from monsoonal flooding in Bangladesh using hydrographic, GPS, and Gravity Recovery and Climate Experiment (GRACE) data, J. Geophs. Res., 115, B08407, https://doi.org/10.1029/2009JB007018, 2010.
Steigenberger, P., Hugentobler, U., Lutz, S., and Dach, R.: CODE contribution to the first IGS reprocessing campaign, Technical Report 1/2011, IAPG/TUM, 2011.
Swenson, S., Chambers, D., and Wahr, J.: Estimating geocenter variations from a combination of GRACE and ocean model output, J. Geophys. Res., 113, 8410, https://doi.org/10.1029/2007JB005338, 2008.
Tapley, B.D., Bettadpur S., and Watkins, M.: The gravity recovery and climate experiment: mission overview and early results, Geophys. Res. Lett., 31, L09607, https://doi.org/10.1029/2004GL019920, 2004.
van Dam, T., Wahr, J., and Lavallee, D.: A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe, J. Geophys. Res., 112, B03404, https://doi.org/10.1029/2006JB004335, 2007.
Wahr, J., DaZhong, H., and Trupin, A.: Predictions of vertical uplift caused by changing polar ice volumes on a viscoelastic Earth, Geophys. Res. Lett., 22, 977–980, 1995.
Wahr, J., Molenaar, M., and Bryan, F.: Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE, J. Geophys. Res., 103, 30205–30229, 1998.
- Abstract
- Introduction
- Methodology
- Greenland and continental GPS-site comparison
- ICESat and GRACE mass changes
- Global major hydrological basin comparison
- Altimetry satellite orbits
- Discussion and outlook
- Data availability
- Appendix A
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Methodology
- Greenland and continental GPS-site comparison
- ICESat and GRACE mass changes
- Global major hydrological basin comparison
- Altimetry satellite orbits
- Discussion and outlook
- Data availability
- Appendix A
- Author contributions
- Competing interests
- Acknowledgements
- References





