2.1 The Lago Buenos Aires moraines

Lago Buenos Aires in Argentina (Lago General Carreras in Chile) is a large proglacial lake, around 100 km long and 5–20 km wide; it is oriented east–west at 46^∘ S (Fig. 1). The present climate of the area is temperate, with an average annual precipitation of 100 mm yr⁻¹ and temperatures between 4 and 14 ^∘C, producing open steppe vegetation. On the eastern edge of the lake, a series of frontal moraines are nested from the youngest close to the lake to the oldest 50 km further east. The chronology of these moraines has been studied: the five innermost moraines (Fenix 1–5) are Last Glacial Maximum (LGM) in age (Douglass et al., 2006; Kaplan et al., 2004). Singer et al. (2004) dated lava flows interbedded with six of the intermediary moraines (Moreno 1–3 and Deseado 1–3) and showed that they range in age between 109 and 760 ka. Finally, six moraines (Telken 1–6) in the outermost part of the system were likely deposited between 760 and 1016 ka. Mercer and Sutter (1982) showed that the oldest glaciogenic sediments we find in the area are 6 Ma and consist of tills interbedded with lava flows that preserved them from erosion. Cosmogenic nuclide exposure dating of boulders supports the assertion that erosion and degradation of older moraines in this region yields erroneously young ages (Hein et al., 2009; Kaplan et al., 2005). Recently, Hein et al. (2017) used exposure dating of cobbles on outwash related to the Moreno moraines to show that they were constructed at ca. 260–270 ka during marine isotope stage (MIS) 8. For this study, we further refined the chronology by providing direct age constraints for the Deseado 1, Deseado 2 and Telken 5 moraines (see Sect. 2.2).

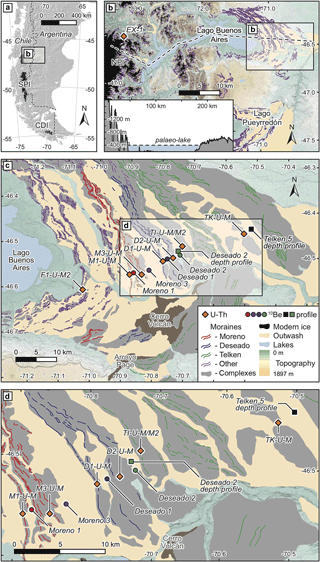
Figure 1Map of the study area adapted from Bendle et al. (2017). (a) Southern South America showing the location of Lago Buenos Aires. The three main contemporary ice masses in Patagonia are also shown: the Northern (NPI) and Southern Patagonian Ice Field (SPI) and the Cordillera Darwin Ice Field (CDI). (b) Inset shows a west–east transect through the study area from the Patagonian Andes to the frontal moraine systems of the proglacial lake (adapted from Kaplan et al., 2009); sample locations as per (a). Panels (c) and (d) show the series of frontal moraines sampled in this study. Silt samples are shown by red circles and cobbles and profiles for cosmogenic analysis are shown in blue; the glacial flour sample at the mouth of Los Exploradores glacier is shown, and the extent of the present day ice field is shown in black. Successive glaciations have formed the large overdeepening in which the proglacial lake has formed.

Download

U and Th samples were taken from silty beds inside the moraines several meters below the surface in order to avoid potential post-depositional modifications, such as weathering or dust inputs (see picture in the Supplement). In addition to moraine samples, a glacial flour sample was taken at the front of the Los Exploradores glacier in Laguna San Rafael National Park to estimate the initial U–Th composition of silts found in the moraines (Fig. 1). This glacier covers part of the total catchment draining into Lago Buenos Aires. Consequently, it is unlikely to be representative of the entire basin but provides an estimate of the initial composition of silts after comminution.

2.2 ¹⁰Be methodology

2.3 U–Th methodology

3.1 Cosmogenic ¹⁰Be and deposition ages

The results of ¹⁰Be analyses are shown in Fig. 2 and Tables 2 and 1. Refer to the Supplement for more details on the profile age results.

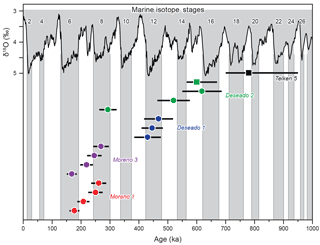
Figure 2¹⁰Be exposure ages from outwash surface cobbles (circles) and modeled depth profiles (squares) for five of the Lago Buenos Aires moraines. Depth profile uncertainties are 1σ. Symbols and colors are the same as in Fig. 1. The δ¹⁸O benthic stack record from Lisiecki and Raymo (2005) is also plotted, and gray shading shows glacial stages.

Download

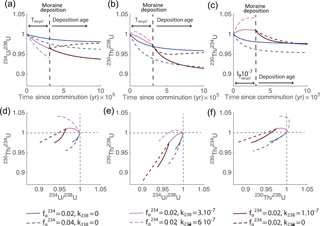
Figure 3Solutions to Eq. 3 that we use as the theoretical framework to analyze our data for different values of f_α and k₂₃₈ (we consider $k_{\mathrm{234}}/k_{\mathrm{238}}=\mathrm{1.4}$ and $k_{\mathrm{230}}/k_{\mathrm{238}}=\mathrm{0.5}$). The time evolution of ²³⁴U∕²³⁸U (a), ²³⁰Th∕²³⁸U (b) and ²³⁰Th∕²³⁴U (c) activity ratios. The vertical dashed line represents an event through which the weathering intensity varies: this corresponds in our case to the time of sediment remobilization. Our ¹⁰Be exposure ages give the time elapsed since this event (shown by the dashed vertical line), whereas the U–Th data indicate the duration of the first phase since comminution and remobilization (from the x axis origin to the dashed vertical line). (d, e and f) The co-evolution of the ratios in (a), (b) and (c), respectively. Different scenarios are plotted corresponding to different f_α values and weathering intensities to illustrate potential patterns in the comminution weathering model (see legend and Sect. 2.3.1). Observing these figures helps in understanding the range of variations in the different activity ratios and the effect of each parameter (α recoil and weathering) on these ratios before and after the remobilization of sediments.

Download

Table 1Cosmogenic ¹⁰Be nuclide data for outwash surface cobbles and depth profile samples. Moreno 1 and 3 data are already published in Hein et al. (2017).

Download Print Version | Download XLSX

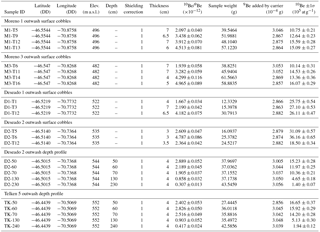
Table 2Modeled exposure ages for outwash surface cobbles and depth profile samples (see main text and the Supplement for details on profile modeling). Moreno 1 and 3 ages have been already published in Hein et al. (2017). Bold values are the oldest samples for each outwash that we consider to be the most representative deposition age of the moraine (see Sect. 3.1 for details).

Download Print Version | Download XLSX

Eight surface cobbles from outwash relating to the Moreno 1 and 3 moraines yielded ¹⁰Be exposure ages ranging from 168–269 ka (Hein et al., 2017). To these we add six more surface exposure ages and two depth profile ages from outwash related to the Deseado and Telken moraines. Three cobbles from Deseado 1 produced relatively tightly clustered exposure ages of 430–468 ka. A cobble from the ice-distal Deseado 2 outwash yielded a much younger, stratigraphically inconsistent age of 293 ka (sample D2-T12), similar to the Moreno ages. Two further cobbles from the Deseado 2 outwash yielded ages of 520 and 618 ka, the oldest of which agrees within errors with a modeled depth profile age of 600 ka ($+\mathrm{70}/-\mathrm{35}$ kyr) from the same outwash unit. The agreement between older ages from surface cobbles and the Deseado 2 depth profile is unsurprising given that modeling suggests that surface erosion (<0.2 cm ka⁻¹) and inheritance within the outwash sediments (<2.10⁴ atom g⁻¹) was relatively low (see the Supplement). There are a number of factors that can result in some age scatter within outwash surface cobbles, including surface deflation and up-freezing of clasts (Darvill et al., 2015; Hein et al., 2017). Moreover, Hein et al. (2009, 2017) suggested that the oldest surface exposure ages from outwash in this region will most closely relate to deposition age. The D2-T12 sample is >200 kyr younger than the other Deseado 2 cobbles, and it is likely that this cobble was either deposited at a much later time (perhaps during Moreno-stage glaciation, although the difference in altitude makes this unlikely) or was not in situ. The close agreement between other Deseado 2 ages supports the removal of D2-T12 as an outlier. Finally, a modeled depth profile through outwash relating to the Telken 5 moraine produced an age of 780 ka ($+\mathrm{170}/-\mathrm{80}$ kyr, 1σ confidence interval), with relatively low surface erosion (<0.1 cm ka⁻¹) and inheritance (<6.10⁴ atomg g⁻¹). This age is within the lower range of 760–1016 ka known from radiometric ages (Singer et al., 2004). Sensitivity tests showed that modifications of the a priori values of erosion rates and inheritance lead to insignificant changes in the resulting age.

3.2 Evaluation of the U–Th chemical procedure with SEM images

For three samples taken randomly, we looked at SEM images after 50 µm sieving and preparation (Fig. 4) to assess the effects of our chemical and mechanical treatment. We were particularly interested in whether secondary phases could remain after processing and if the primary silicates could have been altered by this treatment. The minerals observed are mainly quartz, feldspars and micas corresponding to the lithology of the Andes in these latitudes. We list below the main observations.

• No trace of carbonate, organic matter or oxides were observed in samples that underwent the entire protocol. Prior to treatment, we only note the presence of oxides (Fig. 4b). This does not, however, preclude the presence of carbonate or organic matter since a difference in mass before and after steps 2 and 5 of the protocol was observed. Therefore, the protocol seems efficient at eliminating carbonates, oxides and organic matter.

• Samples were generally cleaner after preparation. This is because ≤4 µm fractions containing mainly clays were removed by Stokes settling. However, clays are still observed in the samples after preparation (see Fig. 4b and c), mainly agglomerated around primary grains as clay pellets. In one sample, up to one-third of the grains have clay pellets. These clays could have been precipitated directly at the surface of the grains during weathering or agglomerated subsequently. It is difficult to fully eliminate the clays and a potential bias could be introduced if too many clays remain in the sample. This potentially limits the application of comminution ages to samples with a very low amount of clays, since their complete removal is currently not possible.

• Most micas show surfaces having experienced weathering (Fig. 4d). The shapes observed are typical of weathering both before and after the protocol. This shows that our silt samples have experienced weathering and that it could potentially have affected U–Th disequilibrium.

• Following the preparation protocol, two feldspar grains in one sample displayed evidence of corrosion (Fig. 4e and f). While this damage could be associated with alteration of the primary silicates during leaching, these are the only two corroded grains visible in the samples we tested. Since the corrosion pits are smaller than 4 µm and all the grains are larger than 4 µm in our samples, ubiquitous damage would be observable on other grains. As such, we assume that primary mineral corrosion during the protocol is minimal.

Figure 4Scanning electron microscopy (SEM) images of selected samples. (a) Overview of a sample after the preparation process described in Sect. 2.3.2. Grains vary in size and shape between 4 and 50 µm and are angular to subangular. White grains are heavy minerals such as zircon or oxides. (b) The same sample before 50 µm sieving. The only notable difference is the presence of clays. (c) Zoomed image of a mineral grain covered in clay pellets that were not removed by the preparation process. (d) Mica grains with cauliflower facies, which is characteristic of weathering. (e, f) Feldspar grains with corroded surfaces. It is unclear whether these corrosion features result from geological processes or the sampling procedure, but they were only observed twice.

Download

3.3 U–Th – f_α – age

U–Th results are shown in Fig. 5 and Table 3. (²³⁴U∕²³⁸U) values from moraines display little variation, ranging from 0.95 to 0.97, while glacial flour has a composition of 1.007 and is close to equilibrium. For the moraine samples, a general decrease in (²³⁴U∕²³⁸U) is observed with time, though with significant noise. (²³⁰Th∕²³⁸U) values mostly vary between 0.94 and 0.97 with the youngest moraine sample (F1-U-M2, Fenix moraine) having a composition around 1. Similarly, (²³⁰Th∕²³⁴U) values mostly range from 0.99 and 1.01, with the youngest moraine around 1.03. Again, an overall decrease in (²³⁰Th∕²³⁴U) is observed with time. The glacial flour is close to equilibrium compositions with $({}^{\mathrm{230}}\mathrm{Th}/{}^{\mathrm{238}}\mathrm{U})=\mathrm{1.02}$ and $({}^{\mathrm{230}}\mathrm{Th}/{}^{\mathrm{234}}\mathrm{U})=\mathrm{1.01}$. Specific surface areas vary from 1.5 to 7 m² g⁻¹, which is typical for this kind of sample, and the fractal dimensions range from 2.45 to 2.6. The recoil loss factors f_α calculated using Eq. 4 are between 0.005 and 0.025, with no observable trend with time.

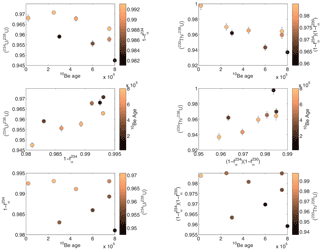
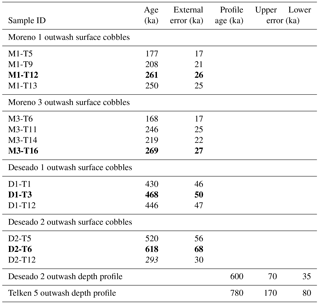
Figure 52-D cross plots of ²³⁴U∕²³⁸U and ²³⁰Th∕²³⁸U activity ratios, associated recoil loss factors ($\mathrm{1}-f_{\mathit{\alpha }}^{\mathrm{234}}$) and $(\mathrm{1}-f_{\mathit{\alpha }}^{\mathrm{234}})\times (\mathrm{1}-f_{\mathit{\alpha }}^{\mathrm{230}}$), and ¹⁰Be exposure ages. Symbol colors represent the third parameter in each plot. The sorting observed in the symbol colors helps to explain the noise associated with the other two parameters. In particular, the scatter in the decrease of the activity ratios over time can be largely explained by the variability in the recoil loss factor (top left plot). The plots also let us assume that the variability in the weathering coefficients could be low; otherwise a residual dispersion would be observed. In all cases, error bars are smaller than the size of the dots.

Download

Table 3U–Th concentrations, activity ratios and BET data (specific surface areas, fractal dimensions and calculated recoil loss factors). Duplicates are also shown, two for the whole process (including sieving, leachings, HF digestion and chromatography) and one for HF digestion and chromatography. The samples are sorted by deposition age (F1: Fenix, M1: Moreno 1, M3: Moreno3, D1: Deseado 1, D2: Deseado 2, TI: Telken 1, TK: Telken 5).

Download Print Version | Download XLSX

Handley et al. (2013a) analyzed only a few samples with the gas adsorption technique to characterize the specific surface area and f_α. We analyzed every sample with this technique, highlighting the consistency of the noise in (²³⁴U∕²³⁸U) and the dispersion in f_α derived from specific surface area (Fig. 5). The relationship between (²³⁴U∕²³⁸U), f_α and age is described by a surface in three dimensions. In other words, the noise observed in the (²³⁴U∕²³⁸U) age diagram around the general decreasing pattern is in large part associated with the dispersion of f_α. This suggests that specific surface area data are consistent and reliable or that, if a bias exists in these data, it is systematic. Such a systematic bias would arise from a rather random event due to sample processing, so this latter explanation seems unreasonable. We conclude that the specific surface area determination based on the gas adsorption technique is valid to evaluate the recoil loss factor in the U–Th comminution age theory.

We observe that (²³⁰Th∕²³⁴U) is larger than (²³⁴U∕²³⁸U) and (²³⁰Th∕²³⁸U) has comparable compositions to (²³⁴U∕²³⁸U). As mentioned in Sect. 2.3.1, this observation is incompatible with a simple comminution age model (only α recoil). An enrichment of ²³⁰Th compared to ²³⁴U could be the imprint of weathering on silts found in the moraines. Similarly, the incompatibilities of (²³⁴U∕²³⁸U) and f_α in the framework of the simple comminution age model suggest that weathering must be considered. In the comminution age theory as described by DePaolo et al. (2006), 1−f_α must always be lower than (²³⁴U∕²³⁸U), and for a sample old enough to have reached steady state, $({}^{\mathrm{234}}\mathrm{U}/{}^{\mathrm{238}}\mathrm{U})=\mathrm{1}-f_{\mathit{\alpha }}$. This is not what we observe, similarly to Handley et al. (2013a). However, as described in Sect. 2.3.1 such an observation can be explained if weathering is considered and k₂₃₄≥k₂₃₈.

Given the large disequilibrium of the youngest samples in (²³⁴U∕²³⁸U) and in (²³⁰Th∕²³⁴U) (Table 3 and Fig. 5) and the fact that the glacial flour (the most probable initial composition for the moraine silts) is close to equilibrium, we cannot ignore the pre-depositional history (i.e., before deposition in the moraines). Based on a starting value close to equilibrium, the disequilibrium values measured here cannot be reached in only 20 or even 200 kyr. Since our estimations of the f_α seem consistent and reliable, this requires consideration of a pre-depositional history involving weathering with a different intensity than during the post-deposition history.

3.4 Pre-deposition history and Monte Carlo analysis

We attempt to constrain the pre-depositional history using a Monte Carlo analysis. The results show an inverse relationship, with the greatest probability for $k_{\mathrm{238}}^{\text{pre}}/k_{\mathrm{238}}^{\text{post}}$ between 2 and 3 and a recycling time between 100 and 200 kyr. The optimal values of k₂₃₄∕k₂₃₈ and k₂₃₀∕k₂₃₈ associated with this solution describe an anticorrelation with $\mathrm{1.2}\le k_{\mathrm{234}}/k_{\mathrm{238}}\le \mathrm{2}$ and $\mathrm{0.01}\le k_{\mathrm{230}}/k_{\mathrm{238}}\le \mathrm{0.8}$ (Fig. 6). These parameters are, however, poorly constrained by the inversion process.

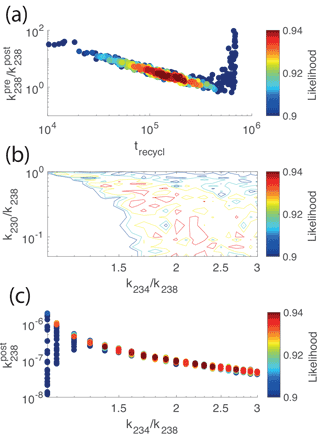
Figure 6Results of Monte Carlo simulations for the U–Th data. The same Monte Carlo simulations were conducted for different fixed values of k₂₃₄∕k₂₃₈ and k₂₃₀∕k₂₃₈ (see Sect. 2.3.5). For each simulation we estimated the optimal solution for $k_{\mathrm{238}}^{\text{pre}}$, $k_{\mathrm{238}}^{\text{post}}$ and recycling time (pre-deposition duration, after comminution), i.e., the solution with the lowest misfit between measured and calculated activity ratio data. We used this misfit to calculate a likelihood between 0 and 1 (see Eq. 5), as shown by the color map (red is lower misfit, blue is higher misfit; stretched to fit our results). The larger the likelihood, the closer to the data the solution is, so the more likely the set of parameter values. (a) The ratio $k_{\mathrm{238}}^{\text{pre}}/k_{\mathrm{238}}^{\text{post}}$ as a function of the recycling time. Each dot is one Monte Carlo solution. The optimal solution (red dots) is for 3 times stronger weathering before deposition and a recycling time of 100 kyr. (b) Relative weathering intensities of ²³⁴U, ²³⁸U and ²³⁰Th. The relative weathering intensities are poorly constrained, but a relationship can be extracted between their ratios: the larger k₂₃₄∕k₂₃₈, the smaller k₂₃₀∕k₂₃₈ must be. (c) A relation between $k_{\mathrm{238}}^{\text{post}}$ and k₂₃₄∕k₂₃₈ can be extracted, even if both parameters are poorly constrained. The estimation of sediment transfer times using U–Th disequilibria series could be improved with better constraints on the relative mobility of ²³⁴U and ²³⁸U.

Download

Despite the numerous parameters to be constrained, the model converges for key results as shown above. We show in particular that, in the framework of the modified comminution age theory incorporating weathering, as described in Sect. 2.3.1, the silts from the LBA moraines were likely eroded 100 to 200 kyr before being deposited in the moraines and that on average they experienced around 2–3 times more intense weathering during this interval than after deposition (Fig. 6). The best fit corresponding to a recycling time of 180 kyr, a ratio $k_{\mathrm{238}}^{\text{pre}}/k_{\mathrm{238}}^{\text{post}}=\mathrm{2.35}$, $k_{\mathrm{234}}/k_{\mathrm{238}}=\mathrm{1.4}$ and $k_{\mathrm{230}}/k_{\mathrm{238}}=\mathrm{0.6}$, is shown in the Supplement Fig. S5.

4.1 Glacial chronology and perspectives on the control of ice extent in the Patagonian Andes

The new ¹⁰Be exposure ages in this study help clarify the timing of the deposition of several LBA moraines. The oldest outwash cobbles are taken as closest to the age of deposition because depth profiles show that average nuclide inheritance is relatively low and outwash surfaces show evidence of deflation (Hein et al., 2011, 2017). It is possible that even the oldest cobbles underestimate the age of deposition if they have also been exhumed, and we apply no erosion correction to our exposure ages. As discussed in Hein et al. (2017), outwash surface cobbles imply that the Moreno moraines were deposited at ca. 260–270 ka during marine isotope stage 8.

Unlike the Moreno system, surface cobbles from the Deseado moraines appear to date from two different glacial cycles. Exposure ages from Deseado 1 outwash yield relatively tightly clustered ages of 430–470 ka, suggesting that the limit was deposited during MIS 12. The older of two published moraine boulder exposure ages from the Deseado 1 moraine (Kaplan et al., 2005) is consistent with the cobble ages in this study. In contrast, surface cobbles from Deseado 2 outwash yield ages of 520 and 618 ka (excluding the anomalously young D2-T12 age of 293 ka). The dating would be less conclusive without the accompanying depth profile age of 600 ka $+\mathrm{70}/-\mathrm{35}$ kyr. Slight changes in scaling factors (see Sect. 2.2.3) do not affect this finding. Taken together, the oldest surface cobble and depth profile suggest that the Deseado 2 limit was deposited at ca. 600–620 ka. Within errors, the limit may relate to MIS 16. The scatter in ages is interesting given that luminescence dating yielded an even younger age of 123±18 ka for the Deseado 2 limit (Smedley et al., 2016). This scatter may imply greater sediment reworking or a more complex relationship between moraines and outwash in this sequence. The Telken 5 depth profile gave an age of 780 ka $+\mathrm{170}/-\mathrm{80}$ kyr that is stratigraphically consistent within our chronological dataset, but less helpful in determining when the limit was deposited. The error range spans MIS 18–24 (and radiometric datings gave a lower age of 760 ka for the Telken series), with larger probability around MIS 20, so it is possible that the moraine was deposited during MIS 20. Since the entire Telken moraine system must be older than 760 ka (Singer et al., 2004), this implies that Telken 1 to 4 are also that age and that the Telken moraines represent different glacial advances during the same glacial cycle.

In summary, there is a clear pattern in the timing of moraine deposition in which alternate glacial cycles are represented in our chronology: Telken 5 during MIS 20; Deseado 2 during MIS 16; Deseado 1 during MIS 12; and the Moreno moraines during MIS 8. Previous work has shown that the innermost Fenix moraines relate to the Last Glacial Maximum during MIS 2 (Douglass et al., 2006; Kaplan et al., 2004; Smedley et al., 2016). We strongly caution that scatter in surface cobble ages and error ranges in depth profiles may complicate this pattern, particularly for the older limits. Moreover, we did not analyze the enigmatic Deseado 3 moraine and so cannot say whether this relates to the counterparts dated here or intervening glacial stages. However, the dating of the Moreno and Deseado 1 and 2 moraines does imply that the intervening glacial cycle is absent from the record.

The pattern in the timing of moraine deposition around Lago Buenos Aires implies that there are a few glacial cycles that are either not recorded in this area or have been erased or removed. Either the ice lobe did not advance during alternate glacial cycles, or it advanced to similar or less extensive positions so that moraines and outwash were then removed by the following advance. A similar pattern was observed by Hein et al. (2009, 2011) for the Lago Pueyrredón ice lobe 100 km to the south, so there could be a regional driver of alternate glacial advances. One possibility is that erosion over successive glacial cycles caused entrenchment of ice lobes within large basins on the eastern side of the Patagonian Ice Sheet (Kaplan et al., 2009). This erosion model has been linked to the pattern of nested limits seen across the former ice sheet (Anderson et al., 2012; Kaplan et al., 2009) but may be more complex if only alternate cycles are represented in the moraine record. Alternatively, a purely climatic forcing could have caused alternate strong advances, although there is no simple relationship between available climate records and alternate glacial advances at Lago Buenos Aires. A complex erosion–climate feedback mechanism may determine when or how far glacial advances occurred in this region, but more detailed glacial models are required to further test such a model.

The chronology presented here suggests that moraine reworking has probably occurred in the area and/or that glacial erosion in the Andes may feed back into the glacial lobe advance to produce this observed pattern of absent intervening glacial cycles. Regardless, this chronology allows us to broadly constrain deposition ages of moraines targeted for U–Th analysis, which may in turn inform sediment recycling times between preserved moraines.

4.2 Implications for sediment recycling, chemical weathering, climate and their interactions in proglacial systems

Following the conclusions of Handley et al. (2013a), the residence time of 100–200 kyr could be an artifact due to an addition of old dust. In our area, when a new moraine is being formed, the older sediments are on the east, whereas the dominant winds come from the west. It is therefore unlikely that these winds could add older material to that being deposited.

The long time estimated using the whole set of data and the Monte Carlo simulations, along with the absence of inheritance in the ¹⁰Be data, suggest that the sediment was not exposed at the surface in the proglacial system before being deposited in its moraine. This implies that the sediment must have been buried, either in the proglacial lake or within a sedimentary pile (moraine, till, channel, etc., at least a few meters below the surface) before final deposition.

The dated sediment was most probably eroded during glacial periods, as erosion rates are likely much larger than during an interglacial. Likewise, deposition in an end moraine occurs during a glacial period. This means that the sediment deposited in the moraine may spend on average as long as 100–200 kyr in the proglacial system (till, lake sediments, etc.) before being deposited in the moraines. Hence the sediment eroded during a glacial period is on average deposited in the frontal moraine during the next glacial cycle. Using postglacial sediment budget and reservoir theory, Hoffmann and Hillebrand (2016) modeled the residence time of sediments in a periglacial system in the Canadian Rocky Mountains and also found a time of 100 kyr. This average residence time implies that a fraction of the sediment deposited in a moraine may have been produced during the same glacial cycle with another fraction being much older.

This time appears to be long. However, our measurements of cosmogenic exposure ages using ¹⁰Be nuclide concentrations in outwash cobbles and profiles suggest that the preserved moraines represent every other glacial cycle, indicating an advance over the proglacial sediment of one or two previous advances. Moreover, it has been shown that proglacial lakes occupying overdeepenings are filled following deglaciation (Eyles et al., 1991; Houbolt and Jonker, 1968). The lakes are filled with sediments during interglacial periods and emptied during the subsequent glacial periods. These processes imply sediment erosion and deposition over a full glacial–interglacial cycle, which is consistent with both ¹⁰Be and U–Th disequilibrium data.

We also obtain a weathering rate that is 2–3 times higher during the 100–200 kyr of the pre-depositional phase than after deposition. Based on the argument above, these sediments are exposed to water in the proglacial system before deposition in the moraine. Authors such as Anderson (2005) have shown that proglacial environments favor weathering. Since weathering rate is a time-dependent parameter (White and Brantley, 2003), the calculated recycling time of 100–200 kyr likely has a non-negligible impact on weathering fluxes.

Understanding how sediments are evacuated and transported to the oceans and when they experience weathering would help to quantify the relationships between erosion and climate. In particular, if 100 to 200 kyr are needed to escape the periglacial area, important lags could be observed between an erosional forcing and the weathering and climate response. This suggests that measured weathering variations could have occurred over the last glacial–interglacial cycles or could have been smoothed and/or damped because of a lag in the sediment transport. Estimating these lag times would help in understanding the relationships between erosion, climate and marine biogeochemical cycles. Erosion rates can be determined using thermochronology or cosmogenic isotopes. Sedimentation rates in the ocean can also be estimated using marine core dating methods. The link between erosion and sedimentation is poorly known (Sadler, 1981), especially because the transport times are poorly constrained. The transport time of 100 to 200 kyr presented here suggests that the pathway between initial erosion and deposition is potentially complex. An effort to constrain these transport times appears to be potentially fruitful to reveal the actual link between erosion and sedimentation rates and climate.

4.3 Perspectives on comminution age method and its applications to characterize sediment transfer

Our data let us estimate only a mean recycling time for moraine sediment (the fine silty fraction). Here we have discussed it in terms of the recycling of the previous glacial cycle moraine, but it could also be interpreted as a mixing of much older, deeper, reworked sediment with new freshly eroded sediment. In other words, we do not quantify the amount of sediment escaping the proglacial system or the amount of sediment rapidly deposited in the moraine after erosion. It would be beneficial to think about age distributions and not only mean ages. However, this necessitates being able to measure U–Th disequilibrium on single grains, which remains an analytical challenge (Bosia et al., 2018).

Quantifying or reducing the effects of weathering remains a major challenge. Pure primary minerals with no clays would minimize these secondary processes. To this end, working on pure zircon grains could be an option. This would require improved mineral separation methods for fractions smaller than 50 µm. One would also have to assume that comminution effectively occurred on such a heavy mineral and that there is no initial disequilibrium (a problem being that zircons are much more enriched in U than the surrounding minerals).