the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Initial insights from a global database of rainfall-induced landslide inventories: the weak influence of slope and strong influence of total storm rainfall
André Stumpf
Jean-Philippe Malet
Marielle Gosset
Taro Uchida
Shou-Hao Chiang
Rainfall-induced landslides are a common and significant source of damages and fatalities worldwide. Still, we have little understanding of the quantity and properties of landsliding that can be expected for a given storm and a given landscape, mostly because we have few inventories of rainfall-induced landslides caused by single storms. Here we present six new comprehensive landslide event inventories coincident with well identified rainfall events. Combining these datasets, with two previously published datasets, we study their statistical properties and their relations to topographic slope distribution and storm properties. Landslide metrics (such as total landsliding, peak landslide density, or landslide distribution area) vary across 2 to 3 orders of magnitude but strongly correlate with the storm total rainfall, varying over almost 2 orders of magnitude for these events. Applying a normalization on the landslide run-out distances increases these correlations and also reveals a positive influence of total rainfall on the proportion of large landslides. The nonlinear scaling of landslide density with total rainfall should be further constrained with additional cases and incorporation of landscape properties such as regolith depth, typical strength or permeability estimates. We also observe that rainfall-induced landslides do not occur preferentially on the steepest slopes of the landscape, contrary to observations from earthquake-induced landslides. This may be due to the preferential failures of larger drainage area patches with intermediate slopes or due to the lower pore-water pressure accumulation in fast-draining steep slopes. The database could be used for further comparison with spatially resolved rainfall estimates and with empirical or mechanistic landslide event modeling.
- Article
(2924 KB) - Full-text XML
-
Supplement
(2947 KB) - BibTeX
- EndNote
Landslides associated with heavy rainfall cause significant economic losses and may injure several thousand people a year worldwide (Petley, 2012). In addition, the frequency of landsliding increases with the frequency of extreme rainfall events (Kirschbaum et al., 2012), which is expected to be enhanced by global climate change (Gariano and Guzzetti, 2016). Landslides are also recognized as a major geomorphic agent contributing to erosion and sediment yield in mountainous terrain (Blodgett and Isacks, 2007; Hovius et al., 1997). Yet, constraining quantitative relationships between landslides and rainfall metrics remains difficult.
There is limited theoretical understanding of how rainfall, through water infiltration in the ground, can increase pore-water pressures and trigger failures (Iverson, 2000; Van Asch et al., 1999). Therefore, a variety of mechanistic models have been developed, usually by coupling a shallow hydrological model to a slope failure criterium (Arnone et al., 2011; Baum et al., 2010; Lehmann and Or, 2012; Montgomery and Dietrich, 1994; von Ruette et al., 2013). However, such deterministic approaches require not only appropriate physical laws but also an accurate and fine-scale quantification of several input parameters such as topography, cohesion, permeability, and rainfall pattern (Uchida et al., 2011). In most places, such a level of detailed information is currently unavailable, rendering deterministic approaches hardly applicable.
Data-driven studies have mostly focused on using precise information on individual landslide location and timing to decipher thresholds, typically based on preceding rainfall intensity and duration, at which a landslide would initiate (Caine, 1980; Guzzetti et al., 2008). Although useful for hazard and early-warning purposes (Keefer et al., 1987), these approaches do not address the quantity and properties of landslides that can be triggered by a rainfall event. In order to understand the importance of rainfall on erosion rates or to anticipate landslide hazard associated with emerging cyclones and heavy rainstorms, it is highly desirable to quantitatively relate the properties of a landslide event L (total area, volume, size distribution) to the combination of site susceptibility, s, and rainfall forcing, f, properties, or equivalently to develop scaling relations of the form of
Note that variables in such an equation may be a statistical description at the catchment or landscape scale (being a simple mean or other moments of the distribution), and thus may not describe the fine-scale variability required by mechanistic models. Although being simplified versions of mechanistic models, such scaling laws can be useful to describe average properties of the phenomena, i.e., a population of landslides associated with a constrained trigger. The advantage of statistical or semi-deterministic approaches is that they are able to accurately predict global properties, while circumventing the difficulties of predicting specific local properties of individual landslides. Indeed, such scaling laws would allow prediction in data-scarce regions and possibly at various scales (hillslope scale, catchment scale, region scale, etc). This approach has driven important progress for both the understanding and hazard management of earthquake-induced landslides, thanks to the introduction of purely empirical, physically inspired, or mixed functional relations in the form of Eq. (1) (Jibson et al., 2000; Marc et al., 2016, 2017; Meunier et al., 2007, 2013; Nowicki et al., 2014). This progress has been possible thanks to detailed investigation of individual case studies with comprehensive landslide event inventories (Harp and Jibson, 1996; Liao and Lee, 2000; Yagi et al., 2009) and through their combined analysis as aggregated databases (Marc et al., 2016, 2017; Tanya et al., 2017). By comprehensive event-inventories we mean that all landslides larger than a given size were mapped, and that the spatial extent of the imagery allowed us to observe the landslide density fading away in all direction, tracking the reduction of the forcing intensity of the triggering event, whether shaking or rainfall.
In contrast, few studies on rainfall-induced landslides are based on comprehensive event inventories. Some studies are based on individual landslide information. For example, Saito et al. (2014) studied 4744 landslides in Japan, that occurred between 2001 and 2011, to better understand which rainfall properties control landslide size. This dataset, aggregating a small subset of the landslides triggered by rainfall events, misses the vast majority of landslides. For example, in Japan, Tropical Storm Talas alone caused a similar amount of landslides in a few days. It is, therefore, insufficient for a more advanced statistical analysis. At the global scale, Kirschbaum et al. (2009) presented a catalog containing information on 1130 landslide events worldwide, which occurred in 2003, 2007, and 2008. With this catalog, they underline the correlation between extreme rainfall and landsliding (Kirschbaum et al., 2012). However, such catalogs, mainly based on reports from various kinds, are rarely adequate to constrain the quantity and properties of landslides triggered by a rainfall event. Thus, we consider that neither studies, based on a small sample of individual landslides or on a global-scale analysis, will be able to effectively constrain Eq. (1), and that detailed storm-scale information is needed.
Few case studies rely on fragmentary event inventories (and are briefly reviewed in the next section) but they may contain too few landslides for statistical analyses or may be biased to specific locations (e.g., along roads or near settlements, within weak lithological units, or near rivers), thus complicating the deconvolution of forcing and site influences. However, in theory, satellite imagery allows for comprehensive mapping of landslides larger than the resolution limit, across all catchments affected by a large storm. In practice, obtaining useful images strictly constraining the landsliding caused by a single storm is not always possible, mainly because of cloud coverage, and detailed mapping across vast areas represents a significant work effort. As a result, landslide inventories triggered by rainfall during a whole season or a few years are used for testing mechanistic models (Arnone et al., 2011; Baum et al., 2010).
The purpose for this work is to present a compilation of new and past comprehensive rainfall-induced landslide (RIL) inventories, each containing the landslide population associated with an identified storm. They constitute the core of an expandable database, essential for further research. We first briefly review existing comprehensive and partially complete inventories associated with specific storms. Then we present six new inventories and analyze their statistical properties in terms of size (total area, landslide density), geometry (length, width, and depth), and relation to topographic slopes. We further analyze and discuss these properties with respect to rainfall observations in those cases and conclude on the various insights that can be derived from such an inventory compilation.
2.1 Review of pre-existing datasets
An in-depth literature review revealed that very few comprehensive, digital, RIL inventories have been published, such as the Colorado 1999 and Micronesia 2002 events detailed below. If we look for partial inventories, in which landslides have been mapped comprehensively in limited zones affected by a storm, a few more datasets exist.
For example, Hurricane Mitch hit Central America at the end of 1998 and triggered thousands of landslides across several countries. The rainfall was record-breaking in many places, with rain gauges recording up to 900, 1100, and 1500 mm in Honduras, Guatemala, and Nicaragua (Bucknam et al., 2001; Cannon et al., 2001; Crone et al., 2001; Harp et al., 2002). In the following weeks, the USGS performed a number of aerial surveys, identified the most affected areas in these three countries as well as in El Salvador (where the rainfall amount was less), and mapped a large number of the failures in selected zones. The resolution of their aerial photographs allowed them to distinguish failures down to a relatively small size (<100 m2), but the mapping amalgamated multiple failures into single polygons, and combined very long debris flow paths and/or channel deposits to the source areas. Because of these limitations, we did not investigate this case in detail but note that these inventories may be corrected and used by later studies. Similarly in a number of studies, inventories of all the landslides caused by a given storm in a specific catchment or geographic zone can be found: in Liguria 2000 (Guzzetti et al., 2004), Umbria 2004 (Cardinali et al., 2006), Sicily 2009 (Ardizzone et al., 2012), Peru 2010 (Clark et al., 2016), Thailand 2011 (Ono et al., 2014), and Myanmar 2015 (Mondini, 2017), as well as in Taiwan for 10 typhoons between 2001 and 2009 (Chen et al., 2013). These inventories could not constrain the total landslide response to a storm, but may allow to constrain relationships between landslide properties and local rainfall properties, provided that enough landslides have been mapped for statistical analysis (e.g., >50–100) and without any systematic sampling bias. However, a detailed assessment of these dataset properties and of their relation to rainfall is outside the scope of this study although it would probably interestingly complement our work in the future.
In this study, we analyzed two datasets previously published by the USGS. First, afternoon rain on 28 July 1999 that triggered numerous landslides and debris flows in the Colorado Front Range (Godt and Coe, 2007). Based on aerial photograph interpretation and field inspection, landslides were mapped as polygons containing source areas, debris flow travel, and deposition zones. Initiation points were assumed to be the highest point upslope of each mapped landslide. In 57 out of 328 polygons, multiple initiation points (2 to >15) were mapped for multi-headed polygons (Godt and Coe, 2007). These polygons are among the largest of the inventory and represent 61 % of the total landslide area. The surface of the source areas were often of similar width, suggesting equivalent contribution from each source to the transport and deposit areas, and rendering a manual splitting impractical. Thus, we instead conserve multi-headed polygons and we use the whole landslide area, Al, perimeter, Pl, and number of source, Ns, for each multi-headed polygon to derive an equivalent area and perimeter associated with each source: and . This first-order approach underestimates the perimeter of each component by one width, the segment that would be added for each new subpolygon; however, this underestimation decreases with the length/width ratio of the polygons, and is already below 10 % for . In any case, this assumption does not affect the total area affected, but it changes the landslide frequency-area and frequency-width distributions, and all terms derived from them.
The second dataset contains landslides caused by a summer typhoon in July 2002, mapped exhaustively with aerial photos on the islands of Micronesia (Harp et al., 2004). We digitized the original maps based on strong contrast between red polygons and the rest of the maps. A few artifacts due to this image processing were removed and a few amalgams were split. Again, scarps and deposits are not differentiated.
2.2 New comprehensive inventories of rainfall-induced landslides
We present the mapping methodology and imagery (Table S1 in the Supplement) used to produce six additional inventories. Here we consider landslides as a rapid downslope transport of material, disturbing vegetation outside of the fluvial domain, which we define by visible water flow in the imagery. We also consider individual landslides with a single source or scar areas to avoid amalgamation, and split polygons when necessary. Although the transition between hillslopes and channel may be blurry and in part subjective, the width estimation (cf. Sect. 2.4) will mitigate variations in the transport length, as long as large alluviated or flooded areas are not mapped as landslide deposits. Still the limit between scar, transport, and deposit areas could rarely be detected with the available imagery, and all polygons consider the whole disturbed areas on the hillslopes. Subsets of the inventories in Taiwan 2009 and Brazil 2011 were produced with an automatic algorithm, and then edited and corrected manually, while all others were manually mapped.
In 2008 around the Brazilian town of Blumenau, several days of intense rainfall at the end of a very wet fall triggered widespread landsliding and flooding, with some partial inventories published in the Brazilian literature (Camargo, 2015; Pozzobon, 2013), which were not reported in the international literature. The detection and manual mapping of landslides as georeferenced polygons was primarily done with a pair of Landsat 5 cloud-free images (1 February 2009 and 2 March 2008). The coarse resolution (30 m) of the images allowed us to only locate vegetation disturbances and accurate landslide delineation was only possible for the largest events. Therefore, we used extensive high-resolution imagery available in Google Earth (over >90 % of the area of interest, AOI) acquired in May–June 2009 in most areas, and in 2010–2012 elsewhere, where scars were still visible. To avoid mapping post-event landslides, we only mapped the ones corresponding to vegetation radiometric index (e.g., NDVI) reduction for the pair of Landsat 5 images, present even for subpixel landslides (e.g., 10 m×5 m). Thus, the landslide mapping could be confirmed for ∼90 % of the mapped polygons, and industrial digging or deforestation occurring on steep slopes could be avoided. This approach avoids amalgamating groups of neighboring landslides and allows for the mapping of very small landslides (∼1 pixel in Landsat 5 images). However, some detailed field mapping in the surrounding of Blumenau reports up to twice the number of landslides that we observed (Pozzobon, 2013), indicating that we still miss a substantial number of small events. Nevertheless, these landslides must be quite small (not visible in ∼1 m resolution imagery) and likely do not affect any of our statistics (area, volume, slope) apart from the total number of landslides.
The same approach was used to map the intense landsliding caused by a few days of intense rainfall between 10 and 12 January 2011 (Netto et al., 2013), in the mountains northeast of Rio de Janeiro. Near Teresópolis, first we used a pan-sharpened (10 m) EO-ALI and 30 m Landsat 7 images from February 2011 for co-registration and ortho-rectification.
>95 % of the slides were cross-checked in Google Earth based on images from the 20 and 24 January 2011 (Fig. 1); and where clouds or no images where available we mapped landslides directly from Google Earth (available over >90 % of the AOI), even if poor ortho-rectification may create geometric distortions. Closer to Nova Friburgo, we used a pair of very-high-resolution GeoEye-1 images (2/0.5 m resolution in multispectral/panchromatic) from 26 May 2010 and 20 January 2011. On these images we applied the methods presented by Stumpf et al. (2014) to classify the whole image, detecting >90 % of the landslides we could manually observe , but also including false positive. Thus, we manually screened the image to remove agricultural fields, inundated areas, channel deposits that were included, and split the amalgamated landslides frequently given the important clusters of landslides in many parts of the image. This correction seems sufficient given that the landslide size distribution for the three subparts of the inventory are consistent (Fig. S1 in the Supplement). Polygons from the automatic classification display a slightly larger equivalent length/width ratio, maybe because some amalgamated polygons have been missed or simply because the classification allows for hollow polygons, biasing upward the length/width estimate based on a perimeter/area ratio (cf. Sect. 2.4).
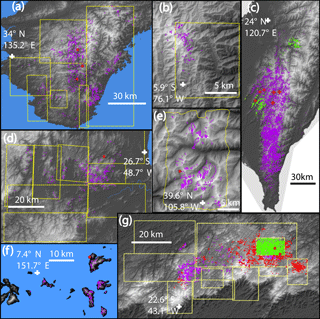
Figure 1Landslides inventory superimposed on digital surface model for the events in Japan 2011 (a), Colombia 2015 (b), Taiwan 2008 and 2009 (c), Brazil 2008 (d), Colorado 1999 (e), Micronesia 2002 (f) and Brazil 2011 (g). Landslides are in purple, rain gauges used in this study are in red dots (and red crosses for Taiwan 2009), and the yellow frames show the availability of high-resolution imagery (Google Earth) used to check or perform the mapping. In (c) the green dots are landslides from 2008, while purple dots are from 2009. In (g) purple, red, and green dots are landslides mapped from EO-ALI, Google Earth, and automatic classification of GeoEye images, respectively.
From 1 to 4 September 2011, Tropical Storm Talas poured heavy rainfall on the Kii Peninsula, in Japan, resulting in several thousands of landslides. For disaster emergency response, the National Institute for Land and Infrastructure Management of Japan (NILIM) mapped landslides across most of the affected areas based mainly on post-typhoon aerial photographs and occasionally on Google Earth imagery (Uchida et al., 2012). Screening antecedent imagery (2010–2011) from Google Earth and Landsat 5, we identified and removed a few hundred pre-Talas polygons, mostly within 5 km of 136.25∘ E/34.29∘ N and 135.9∘ E/34.20∘. With Google Earth we could validate NILIM mapping over about 85 % of the AOI and we added almost 200 polygons in areas were aerial photographs were not taken and split many large or multi-headed polygons that were amalgamated. Some polygons had distorted geometry or exaggerated width, most likely due to poor ortho-rectification of the aerial imagery and/or time constraints for the mapping. We could not systematically check all polygons, but we checked and corrected all polygons larger than 30 000 m2 (3 % of the catalog but representing 45 % of the total area). We consider that the remaining distortions for some of the smaller polygons have minor impacts on the statistics discussed in the next sections.
In Taiwan, we collected landslide datasets associated with the 2008 Kalmaegi (16–18 July) and 2009 Morakot (6–10 August) typhoons, partially described by Chen et al. (2013). For 2008, we compared multispectral composite images and NDVI changes between (30 m) Landsat 5 images taken on the 21 June, 7 July, and 23 July. The image from 7 July is covered by clouds and light fog in many parts but allows us to identify that most places affected by landslides in the last images were still vegetated at this time. Thus all new landslides are attributed to the rainfall from typhoon Kalmaegi. For 2009, landslides were mapped with pre- and post-event FORMOSAT-2 satellite images (2 m panchromatic and 8 m multi-spectral; Chang et al., 2014). To cover most of the island, we mosaicked multiple mostly cloud-free pre-event (14 January, 8 May, 9 May, 10 May, 6 June 2009) and post-event (17 August, 19 August, 21 August, 28 August, 30 August, 6 September 2009) images. For a subsets of the inventory, especially to the east of the main divide, landslides were significantly amalgamated and bundled with river channel alluviation. We thus manually split the polygons and removed the channel areas.
In a few areas with clouds (<5 % of the AOI) in the post-event mosaic, we mapped with Landsat 5 images (from 24 June and 12 September 2009), even if the spatial resolution limit may have censored the smallest landslides in these zones. Special attention was given to the separation of individual landslides by systematically checking and splitting polygons above 0.1 km2 (2 % of the catalog but representing 30 % and 60 % of the total area and volume, respectively). However, it is clear that a number of smaller landslides are missed or merged with large ones; and, therefore, although total landsliding and landslide locations on slopes may be well represented, the size distribution of this catalog must be biased to some extent.
Between 15 and 17 May 2015, heavy rainfall in the mountains above the village of Salgar, Colombia, triggered catastrophic landslides and debris flow (>80 deaths). Landslide mapping was carried out by comparing a (10 m) Sentinel-2 image from the 21 July 2016 and a pan-sharpened (15 m) Landsat 8 image from the 19 July and 26 December 2014. These images were selected for their absence of clouds, good conditions of light, and similarity. High spatial resolution imagery from Google Earth, dated from 31 May 2015, shows fresh scars consistent with our mapping over most of the area (Fig. 1), and we assumed that the remaining landslides (<15 % of the inventory) were also triggered by the same rainfall event.
2.3 Rainfall data
Rainfall data quality and amount are very variable for the different events, from none or one single gauge (for Micronesia or Colombia) to a dense gauge network and potentially weather radar coverage in Japan, Taiwan, and Brazil. Therefore, we selected a simple index that could be obtained for each case in order to discuss potential rainfall controls on the landslide properties. For each case we calculated an estimate of total rainfall, Rt, duration, D, and a peak rainfall intensity over 3 h, I3 (Table 1). Note that these variables do not represent an average value within the whole footprint of the storm, but rather a maximal forcing, usually colocated with the areas where landsliding was the most intense (Fig. 1) and derived mostly from one or a few rain gauges. Thus, these indexes may be taken as storm magnitude. A more detailed analysis of the spatiotemporal pattern of the rainfall and of its relations to the spatial pattern of landsliding is highly desirable, but challenging and is left for a future study.
The estimates from Taiwan and Japan are based on hourly gauge measurements from the Japan Meteorological Agency and Taiwan Institute for Flood and Typhoon research. In each case we took the three closest gauges within 5 to 15 km from the areas with the highest landslide densities (in 0.05 by 0.05∘ window, Fig. S2) and computed their average properties (Fig. 2). Minimum and maximum single gauge measurements give a coarse measure of the uncertainty. A single gauge is available in Micronesia, and we used the hourly rainfall from 1 to 3 July 2002 reported in Harp et al. (2004). For Colorado, we used the hourly rainfall from the rain gauge at Grizzly Peak, closest to the intense landsliding reported by Godt and Coe (2007). For this event, radar data indicate very localized, high-intensity precipitation located on the peaks where the debris flows occurred (Godt and Coe, 2007) and suggests that the single closest gauge is more representative than averaging with the other nearby ones. For the event in Brazil 2008 we considered the total daily rainfall from Luis Alves station (Fig. 1), where more than 130 mm day−1 were accumulated on the 21, 22, and 23 November and 250 mm on the 25, and intensity going up to 50 mm h−1 (Camargo, 2015). These days were also preceded by an abnormally wet period, with November 2008 accumulating ∼1000 mm, 7 times the long-term average for this month. In 2011 in Brazil, hourly rain data at Sitio Sao Paulista report 200 mm in 8 h before gauge failure, while there, and at nearby sites, the cumulative rainfall was ∼280 mm from the 10 to the morning of the 12 January (Netto et al., 2013). For these cases, rain gauges give a trustworthy estimate of the local rainfall, but are not constraining the large-scale rainfall pattern. Last, in Colombia, we could not find data from any nearby rain gauge and we thus use rainfall estimates from the GSMaP global satellite products (Kubota et al., 2006; Ushio et al., 2009) (Fig. S3). Here, the minimum, mean, and maximum rainfall are obtained by considering the triggering storm as the raining period at the time of debris flow occurrence, or the one from the previous day or merging both events, respectively (Fig. S3).
Defining storm duration accurately requires defining thresholds on rainfall intensity over given periods, to delimit the storm start and end. Given the variable quality of our data, we limit ourself to a first-order estimate of the continuous period when rainfall was sustained (i.e., I3>3 mm h−1). We consider these durations accurate within 10 %–20 % for the events with overall hourly data. For the less constrained cases B08, B11 and C15 durations are more uncertain. In any case, for these eight storms, we note a strong correlation between D and Rt and I3 and Rt (for power-law scalings, R2=0.9 and R2=0.8, respectively (Fig. S4). Thus, given that spatial and temporal length scales are often linked in meteorology, the long events causing larger rainfall may also have larger footprints.
Table 1Rainfall data summary, containing the total rainfall, duration and maximum 3 h intensity for each storms. For TW8, TW9 and J11, we indicate the range for the three indexes that could be estimated from three gauges near the zone of maximal landsliding. We cannot perform this analysis for MI2 and C99, and can only assess a range of Rt for B08 and B11. For B08 the question mark indicates that the upper bound of Rt is under-constrained and taken as 115 % of the best estimate. For C15, we indicate by a star that we could only access satellite based rainfall estimates (GSMaP_MVK V04 ungauged products; Kubota et al., 2006; Ushio et al., 2009; see Fig. S3). Reference are as follows, 1: Godt and Coe (2007), 2: Harp et al. (2004), 3: Camargo (2015), 4: Netto et al. (2013) .

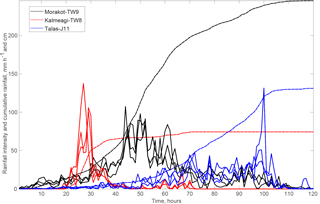
Figure 2Rainfall history for typhoons Kalmaegi (TW8), Morakot (TW9), Talas (J11). For each event, hourly intensity is shown with solid curves for three gauges nearby the area with most intense landsliding (see Fig. 1 for locations). Dashed lines represent the mean cumulative rainfall from the three gauges.
2.4 Landslide area, width and volume
Landslide plan view area and perimeter are directly obtained from each polygon. However, these values represent the total area disturbed, that is the scar, deposit and run-out areas, because a systematic delineation of the scar was not possible from most of the imagery. This means that landslide size statistics are resulting from processes affecting both landslide triggering and run out. Landslide volume, estimated based on area, may also be overestimated for long run-out slides. Therefore, we propose here a simple way to normalize for landslide run out and obtain an estimate of the scar area.
Following Marc and Hovius (2015), we computed an equivalent ellipse aspect ratio, K, using the area and perimeter of each polygons. For polygons with simple geometries, K is close to the actual length/width ratio, but this is a measure that also increases with polygon roughness or branching, and therefore with amalgamation (Marc and Hovius, 2015). Assuming an elliptic shape, polygon area can be approximated by πLW∕4 with L and W being the polygon full length and width, respectively. This allows us to estimate . To validate this geometric method to retrieve landslide width, we systematically measured the width of 418 randomly selected landslides across a wide range of polygon areas and aspect ratios, belonging to four inventories: J11, TW8, B11, and C15. For each polygon, we focused on the upper part of the landslide only, the likely scar, and averaged four width (i.e., length perpendicular to flow) measurements made in arcGIS. The width estimated based on P and A are within 30 % and 50 % of the measured width for 72 % and 92 % of the polygons, respectively (Fig. S5). We do not observe a trend in bias with area nor aspect ratio, except perhaps for the automatically mapped landslide in B11, where high aspect ratio correlates with underestimated width. Thus, for correctly mapped polygons, we can use P and A to derive W and a proxy of landslide scar area, As∼1.5W2. We assume landslide scars have an aspect ratio of 1.5, as it was found to be the mean aspect ratio found across a wide range of landslide size within a global database of 277 measured landslide geometries (Domej et al., 2017). Even if this equivalent scar area may not exactly correspond to the real landslide scar, it effectively removes the contribution of the landslide run out to the landslide size and allows us to compare different size distributions while reducing the impact of variable run-out distances.
We also assessed how using As affects estimates of landslide volumes and erosion, by computing landslide volume with the total landslide area and with As only. In both cases, we used V=αAγ, with α and γ and their 1σ globally derived by Larsen et al. (2010). Given that soil and bedrock slides have different shape and that soil slides are rarely larger than 105 m2 (104 m2 for soil scars; Larsen et al., 2010), we used the “all landslide” parameters (; ) when A<105, and the “bedrock” parameters (; ) for larger landslides. Similarly, we used the soil scars (; ) and bedrock scars (; ) for As<104 m2 and As>=104 m2, respectively (Larsen et al., 2010). Marc et al. (2016) proposed a rudimentary version of such a run-out correction, where they effectively reduced landslide area by a factor of 2 for mixed landslides and of 3 for bedrock landslides, noting that volumes derived in this way were closer to field estimates for large landslides than without correction.
Uncertainties in this approach include the 1σ variability in the coefficient and exponent of the landslide area–volume relations given above, and an assumed standard deviation of 20 % of the mapped area. These uncertainties were propagated into the volume estimates using a Gaussian distribution. The standard deviation on the total landslide volumes, for the whole catalogs or for local subsets, were calculated assuming that the volume of each individual landslide was unrelated to that of any other, thus ignoring possible covariance. Although estimated 2σ for single landslides is typically from 60 % to 100 % of the individual volume, the 2σ for the total volume of the whole catalog is below 10 % for the eight datasets. However, for subsets with fewer landslides and with volume dominated by large ones, typical when we compute the total landslide volume density in a small area (e.g., 0.05∘), 2σ uncertainty reaches 40 %–60 %. We note, however, that these uncertainty estimates do not consider potential errors in the identification of landslides, either missed because of occasional shadows or clouds, or erroneously attributed to the storm. Such uncertainty is hard to quantify but must scale with the area obscured in pre- and post-imagery. In most cases multiple pre- and post-event images mean that obscured areas typically represent less than 10 % of the affected area, and such errors may be between a few to ∼20 % of the total area or volume, depending on whether obscured areas contain a landslide density higher or lower than the average observed throughout the affected area. Last, resolution may not allow us to detect the small landslides and in some cases the landslide number may be significantly underestimates, but not the total area and volume dominated by the larger landslides.
For each inventory, we also estimated the landslide distribution area, that is the size of the region within which landslides are distributed. Based on the landslide inventories we could delineate an envelope containing the overall landsliding. As discussed by Marc et al. (2017), such delineation is prone to high uncertainties as it is very dependent on individual isolated landslides. Thus for all cases, we give a range of distribution area, where the upper bound is a convex hull encompassing all the mapped landslides, while the lower bound is an envelope ignoring isolated and remote landslides (i.e., single or small cluster of landslides without other landslides within 5–10 km), if any. Although the spread can be large in absolute value, both approaches yield the same order of magnitude.
The inventories contain from ∼200 to >15 000 landslide polygons, representing total areas and total volumes (from scars) from 0.2 to 200 km2 and 0.3 to 1000 Mm3, respectively. The triggering rainfalls are characterized by a total precipitation of ∼50 to 2500 mm in periods ranging from 4 h to 4 days, and caused landslides within areas ranging from ∼50 to 10 000 km2. Although the dominant landslide types are soil and regolith slumps, a number of large deep-seated bedrock landslides are also present in the inventories associated to the Talas and Morakot typhoons (Chen et al., 2013; Saito and Matsuyama, 2012). A more detailed description of the landslide types and materials involved was not possible with the available imagery; thus, our analysis does not consider landslide types. In the next sections, we present results obtained from these inventories in terms of landslide size statistics, landslide spatial patterns, and relation to slope, before correlating these landslide properties to rainfall parameters.
3.1 Landslide properties
3.1.1 Landslide size statistics
Frequency size distributions of landslide inventories have typically been fit by power-law tailed distributions, above a certain modal size (Hovius et al., 1997; Malamud et al., 2004). The modes and the decay exponents of these distributions are mainly related to the lithology (mechanical strength) or topographic landscape properties (i.e., susceptibility related) (Frattini and Crosta, 2013; Katz et al., 2014; Milledge et al., 2014; Stark and Guzzetti, 2009). Some authors suggested that this behavior could also be affected by the forcing processes. For example, analyzing earthquake-induced landslide catalogs, it was found that deeper earthquakes, thus with weaker strong-motions, have a smaller proportion of large landslides (Marc et al., 2016). Based on theoretical arguments, it has been proposed that short, high-intensity rainfall could cause pulses of high pore-water pressures at the soil–bedrock transition, initiating mainly small, shallow landslides, while long duration rainfall with high total precipitation could provoke significant elevation of the water table and trigger large, deep-seated landslides (Van Asch et al., 1999). To our knowledge, little empirical evidence has supported these assumptions, and we discuss next how our data compare to these ideas.
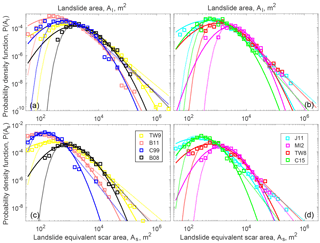
Figure 3Probability density functions of landslide whole area (a, b) and estimated scar area (c, d). To improve visualization we split the 8 inventories in two groups. A Log-Normal and Inverse Gamma Distribution maximum-likelihood estimation for the whole distribution are shown by solid and dashed lines, respectively.
All landslide size distributions present a roll-over and then a steep decay (Fig. 3). The modal landslide area varies between ∼3000 m2 for TW8 and ∼300 m2 for B11, while the largest landslides are ∼0.1 km2 for most events and reach ∼0.4 and 2.8 km2 for J11 and TW9, respectively. The roll-over position certainly relates partly to the spatial resolution and acquisition parameters of the images (Stark and Hovius, 2001) (e.g., for TW8 and B08, where landslides were mostly mapped on a coarse spatial resolution image compared to aerial photographs for C99 and J11). However, mechanical parameters are also expected to influence the roll-over position (Frattini and Crosta, 2013; Stark and Guzzetti, 2009), as suggested by the fact that MI2, mapped with 1 m resolution aerial imagery, has larger modal area than C15, mapped with 10 m Sentinel-2 satellite imagery. Following Malamud et al. (2004), we use maximum likelihood estimation (MLE) to fit the whole distribution with an inverse gamma distribution (IGD) and obtain power-law decay exponents α+1 between ∼2 and 3, consistent with the typical range found in the literature (Frattini and Crosta, 2013; Hovius et al., 1997; Malamud et al., 2004; Stark and Guzzetti, 2009). However, we note that at least three cases, B11, TW9 and C99, poorly follow an IGD, with a break in the distribution occurring in large areas, followed by a very steep decay.
When considering landslide estimated scar sizes, that is essentially a correction to reduce landslide polygon aspect ratio to 1.5, we observe a reduction of the largest landslide size by 2 to 10 times, but a moderate reduction of the modal area. This is consistent with the fact that landslides with long run-out distances are often over represented within the medium to large landslides (Fig. S6). We also note that after the run-out distance variability is normalized, the distribution of C99 agrees better with an IGD. This is not the case, however, for B11 and TW9 that still feature a steepening of their distribution decay (and a divergence from IGD fit) beyond ∼103 and ∼104 m2, respectively. Run out being normalized, this could be an artifact relating to residual amalgamation for TW9, but not for B11, where most landslides were mapped manually and amalgamation was avoided. In these two cases, for the whole landslide area or the landslide scar only, we note that a MLE fit of a log-normal distribution agrees better to the data (based on the result of both the Kolmogorov–Smirnov and the Anderson–Darling test). For other inventories, a log-normal fit is equivalent or worse than an IGD, but we note that the parameters describing the decay of both distributions are highly correlated (Fig. S7). Thus, we take α+1 as a reasonable indicator of the relative proportion of large landslides within the different dataset and do not further explore the functional form of landslide size distribution and its implications, which we consider beyond the scope of this study.
3.1.2 Landslide and slope distribution
For all cases, we computed the frequency of slope angles above 5∘ based on the global 1 arcsec (∼30 m) Shuttle Radar Topography Mission (SRTM) digital surface model (Farr and Kobrick 2000; Farr et al., 2007). In most cases, hillslopes have a distribution clearly independent from valley floors. However, for B08 and MI2, for example, the amount of plains in the study area do not allow for resolving the hillslope distribution. Therefore, for Micronesia we removed all slopes which are less than 10 m above sea level; and for Brazil, we extracted the slope cells in the landslide distribution area but with a mask excluding the wide valley bottoms, allowing us to obtain a hillslope distribution as an approximate Gaussian, with a mode significantly beyond our threshold of 5∘. To focus on the scar area of each landslide polygon, we extracted only the slopes for the highest-elevation pixels representing a surface of 1.5 W2 m2. Then, we computed the probability density function for the landslide-affected area and the whole topography (hereafter the “landslide” and “topographic” distributions) with a normal-kernel smoothing with an optimized bandwidth, as implemented in Matlab. We obtain topographic modal slopes, SM, at 15.5 and 18.5∘ for the gentle landscape of Micronesia and Brazil, while in Japan and Taiwan we reach almost 30∘ (Fig. 4a). The landslide distributions are unimodal, except for C15 that seems to have secondary modes at SM−5 and SM+25, and are systematically shifted towards steeper slopes.
To further quantify the differences in slope sampling between these events, we computed the ratio of probability between the slope distribution of the whole topography and of the landslide-affected area only (PL∕PT, Fig. 4). This ratio represents the tendency of landslide occurrence on a given slope to be more or less frequent than the expected occurrence of this given slope in the landscape. We refer to this as an oversampling or undersampling of the topographic slope distribution. To compare the events in different landscapes, we plot each event against S−SM (Fig. 4b). An important issue is to determine whether the landslide probability can be considered a random drawing from slopes of the topography or not. Given that landsliding affects less than 10 % of the landscape, the sampling of the topography by landslides can be approximated by a Bernoulli sampling. In this case, the central limit theorem gives the 95 % prediction interval as , with N the number of independent draws, here taken as the number of landslide scars. The convergence of N draws to PT within the prediction interval is only valid if N>30, NPT>5, and , implying that only very large samples can be interpreted towards the extremity of the topographic slope distribution, where PT is small.
For all events, we observe that PL is significantly different from a random drawing of the topography with oversampling of the slopes beyond SM and undersampling below it (Fig. 4b). However, we note that for most events the undersampling and oversampling is smaller than a factor of 2. Some cases (C15, J11, and TW8) have stronger oversampling (>4) for but they may not be representative ratios given the limited number of landslides and of slopes this steep (i.e., NPT<5). The scars of C99 clearly depart from this behavior, with undersampling and oversampling of a factor of 10 and 6 at , respectively. B08 has also strong undersampling below SM but has a landslide distribution that rapidly converges to the topographic ones at high slopes.

Figure 4(a) Slope gradient probability distribution for the affected topography (solid) and the landslide scar areas only (dashed), for the eight rainfall events and as a comparison to the Chi-Chi earthquake. (b) Ratio of the two probability distributions against the difference between slope gradient and the modal topography. The ratios are estimated with the PDF averaged within 3∘ bins. Solid circles and dots represent ratios where the landslide probability is beyond or within, respectively, the 95 % prediction interval of the topography distribution. Crosses indicate bins where data are insufficient for the validity of the central limit theorem required to estimate prediction interval.
3.2 Correlation between rainfall metrics and landslide properties
3.2.1 Total landsliding
For the eight inventories, we observe a nonlinear increase in all metrics of total landsliding with the storm total rainfall (Fig. 5). The increase is similar for the total area and volume, and best fit by exponential functions. We observe higher correlations with rainfall, when using the total scar area (R2=0.78), estimated as W2, instead of the total area (R2=0.72). This is mainly due to the very large reductions of area for C99 and B11, where long run-out landslides were dominant (Fig. 5). Correlations are generally higher with volume and also increase when we derive total volume from scar estimates (from R2=0.81 to R2=0.87). Note also that with these scar metrics, the relation to rainfall becomes equally or better fit by a power-law function rather than an exponential function (Fig. 5). This is because when including landslide run out, the total landsliding of C99 and C15 is larger and creates an apparent asymptote, better fit by an exponential function. Last, we note that total volume values may change depending on which A-V scaling relations are used and with which assumptions, and their absolute values may be inaccurate but this should not affect the reported scaling form and exponents, considering that potential biases should be relatively uniform.
Total number of landslides also tends to increase with total rain but the scatter is much larger (Fig. 5). This is at least partly an artifact, given that for C99, MI2, and B11, high spatial resolution imagery allows us to delineate many more small landslides and to mitigate amalgamation, whereas for B08, TW8, and TW9, the limited spatial resolution, the density of landsliding, and our limited ability to split amalgamated landslides lead to an underestimation of the landslide number. Thus, even if landslide number may contain information, quantitative comparisons of the events are biased and we will not further interpret the total number of landslides in the following.
Last, we note that the landslide distribution areas (i.e., the regions within which landslides are distributed) also correlate strongly with the total rainfall. Only considering the eight inventories strongly suggest a power law form. However, based on the dataset reported for Hurricane Mitch, the distribution area was at least 100 000 km2 for maximum total rainfall of about 1500 mm (Cannon et al., 2001). Adding it to our fit, we found that power-law or exponential functions of the rainfall explained a similar amount of the variance, 72 % and 63 %, respectively.
In the next subsection, we compute landslide densities (in % of area), allowing us to study the intra-storm variability in landsliding.
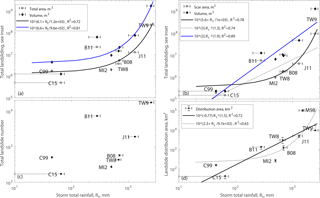
Figure 5Total landsliding in area and volume derived from whole landslides (a) or from scar estimates only (b), total landslide number (c) and landslide distribution area (d) against storm total rainfall. M98 is for Mitch 1998. Horizontal error bars show a range of maximum storm rainfall when available (cf., Table 1). In (a) and (b) 1σ uncertainty in the total volumes and areas, ignoring potential landslide mis-detections (cf. methods), are smaller than the symbols (<10 %). Vertical error bars are based on the range of affected areas in (d), while we could not obtain quantitative uncertainties in the total number (c).
3.2.2 Maximum and mean landslide density
Understanding what controls landslide density is a key objective to better constrain hazards and their consequences. For each storm, we compute the mean landslide density (in area and volume) by dividing total landsliding by the landslide distribution area (Fig. 6a). This density represents the whole affected area and hides important spatial variability (Fig. 1), thus we also compute the maximum landslide density by computing the total landsliding (again in area and volume) within a moving window of 0.05∘ (∼ 25 km2), assigning landslides to a cell based on their centroid locations and selecting the maximal value (Fig. 6b). Given the better correlation obtained above with a run-out normalization, we focus on area and volume densities derived from scar estimates.
The mean landslide densities vary between 0.01 %–1 % and 100–10 000 m3 km−2 but with poor correlation with total rainfall (R2=0.01 and R2=0.46 for area and volume density, respectively). Indeed, given that both total landsliding and distribution area increase strongly with total rainfall, their ratio is relatively independent. In contrast, the maximum landslide scar density and volume density range from 0.1 % to 5 % and 0.002 to 1.5 millions m3 km−2 , respectively, and are strongly correlated with a power-law of total rainfall (R2=0.76 and R2=0.95). We found very similar correlations when computing the local density on a grid of 0.03 or 0.1∘, but degraded correlations when using the whole landslide area to compute landslide density (R2=0.40 and R2=0.69). We also note that, as for the total landsliding, maximum landslide density and volume density are significantly correlated with peak rainfall intensity, I3 (R2=0.58 and R2=0.67, respectively), and duration, D (R2=0.70 and R2=0.73, respectively), although less strongly than with total rainfall.
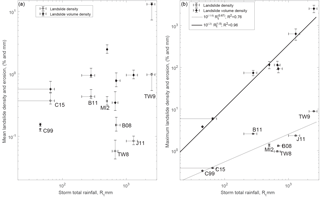
Figure 6Mean landslide density (a) and peak landslide density in a 0.05∘ sliding window (b), against storm total rainfall. Landslide area and volume are derived from scar estimates, i.e., removing run-out contribution. Horizontal error bars show a range of maximum storm rainfall when available (cf., Table 1). Vertical error bars are based on the range of affected area in (a) (the most uncertain term), and represent 1σ uncertainty in the total volume and area density in (b), ignoring potential landslide mis-detections (cf. methods).
3.2.3 Landslide size, run out, and position on slope
The decay exponents of the distribution of landslide area do not correlate significantly with any storm metrics (intensity, duration, or total rainfall; ). However, after run-out normalization, the decay exponents of landslide scar area correlate with all metrics, although with significant scatter (R2∼0.5 Figs. 3, 7). The two largest storms (J11 and TW9) have the lowest exponents (), and thus a large proportion of very large landslides, while the two smallest storms (C15 and C99) have a small proportion of large landslides and large exponents (). However, intermediate cases are very scattered, as B11 and TW8 have similar total rainfall, peak intensity, and duration but very different distribution with and with , respectively. Still, randomly removing one event (i.e., jackknife sampling) we obtained R2 between 0.4 and 0.7, with a similar mean R2 of about 0.5.
The decay exponents of the equivalent aspect ratio (Figs. 3, S6) do not correlate significantly with any storm metrics (intensity, duration, or total rainfall; ). Indeed, long run-out landslides are abundant for the smallest storms, C99 and C15, as well as for the second largest storm, J11, but are relatively rare for other storms (e.g., MI2,TW8, B08), spanning the whole range of storm indexes. Similarly, the mean and modal aspect ratio are similar for all events across all storm metrics, except for C99 which is heavily dominated by debris flow and has a modal aspect ratio >10.
We have observed that almost the eight events behave similarly with respect to the distribution of topographic slopes, not suggesting a strong link with the individual storm properties. The C99 event has a different behavior that may relate to the fact that it was the shortest storm with the smallest total, or that it was the only case occurring in high-elevation terrain with sparse vegetation. C15, the second shortest and smallest storm event may also have strong oversampling about 20∘ beyond SM but the limited number of landslides does not allow us to confirm the significance of this oversampling.
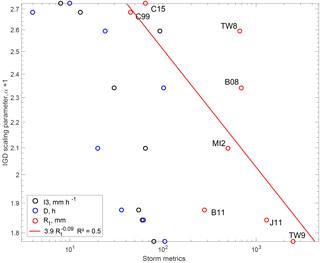
Figure 7Landslide scar size distribution decay exponents against storm total rainfall (red), storm duration (blue) and storm peak intensity (black). The best least-squares fit is shown in red. The reduction of the decay exponents with increasing storm magnitude indicates an increase in the proportion of large landslides relative to small landslides.
4.1 Scaling between rainfall and landsliding
We found that total landsliding, peak landslide density, and the distribution area of landsliding were all best described as increasing as a power-law or exponential function of the total storm rainfall, Rt. Our mechanistic understanding of landsliding predicts that, for a given site, the mechanism leading to failure is the reduction of the normal load and friction due to the increasing pore-water pressure (Iverson, 2000). This requires progressive saturation of the material above the failure plane and depends directly on the total amount of water poured on the slopes. However, we can envision that landscapes may rapidly reach an equilibrium in which all unstable slopes under rainfall conditions frequently occurring would have been removed. In this framework, the rainfall amount relative to the local climate would be more relevant than absolute rainfall, requiring an analysis in terms of deviation from the mean rainfall or in terms of rainfall percentiles (Guzzetti et al., 2008). Although we could not define rainfall percentiles in each area, we note that normalizing Rt by the mean monthly rainfall relevant for each storm, we still find a decent correlation with the peak landslide density, implying climate normalized rainfall variable may be driving landsliding (Fig. S8).
The antecedent rainfall is also expected to play a key role in controlling the saturation level before the triggering storm (Gabet et al., 2004; Godt et al., 2006). However, if the regolith is already close to the field capacity, significant parts of antecedent rainfall may be drained from the regolith within some hours or days (Wilson and Wieczorek, 1995), and as a result, the contribution of past storms may be negligible compared to heavy rainfalls over relatively short time intervals (1–4 days). However, for moderate storms, like C15 or C99, and especially during dry periods when the slopes are saturated below field capacity, the role of antecedent rainfall may be more substantial. Thus, we expect that moderate storms happening after prolonged dry or wet periods may deviate downward or upward from the scaling, respectively. We also note that the abundance of larger and deeper landslides, strongly influencing the total volume or erosion, may depend on deeper water level rather than regolith saturation and thus may be most sensitive to water accumulation over several days rather than a few hours (Uchida et al., 2013; Van Asch et al., 1999). Therefore, although we obtained a good correlation without considering antecedent rainfall, its role should be assessed in future refined scalings. Last, the scaling reported here is based on events where all landslides occurred within a short time frame (few hours to few days), and would not apply to a monsoon setting where landslides occur more or less continuously during several weeks (Dahal and Hasegawa, 2008; Gabet et al., 2004), driven by continuous, heavy but unexceptional, rainfall. Indeed, in a long period with fluctuating rainfall such as the monsoon, drainage and storage of water will certainly not be negligible and the derivation of a soil water content proxy will be necessary (Gabet et al., 2004).
The strong correlation between Rt and Ad suggests that storms able to generate greater amounts of rainfall also tend to deliver a sufficient amount of rain over broader areas. For tropical storms and hurricanes (5 out of 9 cases in Fig. 5d) a number of studies (Jiang et al., 2008) found that the maximum inland storm total rainfall (i.e., Rt for us) correlated well (R>0.7) with a rainfall potential defined as the product of storm diameter and storm mean rainfall rate within this diameter over storm velocity, each term measured 1–3 days before the storm made landfall. It was also generally observed that rainfall intensity is higher closer of the storm core, thus potentially tightening the link between Rt and a given storm radius with intense rainfall and high landslide probability. These observations would imply linear proportionality between Rt and Ad and could be consistent with the observed power-law trend (exponent 1.5; Fig. 5), especially if some further links between Rt and mean storm intensity or velocity exist. Potential links between Rt and Ad for smaller-scale storms (C99, C15, B08, and B11) are harder to interpret, and we cannot exclude that it is a coincidence allowed for by our small number of events.
In any case, the broader zone is not likely to receive homogeneous rainfall amount, decoupling mean landslide density from storm maximum strength (Fig. 6a). The variability in rainfall within these extended zones is likely a main control on the spatial variability in landslide density, although lithological properties or slope distribution may also matter. Indeed lithological boundaries or a lack of steep slopes can sometimes explain spatial variability in landsliding, but not all of it (e.g., Fig. S9). In any case, it seems clear that to predict the spatial variability of landsliding, the rainfall spatiotemporal pattern is a primary requirement. The good correlation between storm total rainfall and peak landslide density is encouraging and suggests that, as most mountainous regions may have sparse instrumental coverage, the use of satellite measurements (Huffman et al., 2007; Ushio et al., 2009) or meso-scale meteorological models (Lafore et al., 1997) may be required to understand the spatial pattern of rainfall-induced landsliding.
A few nonlinear scalings between total landsliding and total rainfall have been reported at the catchment scale, but were derived from datasets not easily comparable to the one presented in this study (Chen et al., 2013; Marc et al., 2015; Reid, 1998). The details of this scaling are of importance in order to understand the impact of extreme rainfall events and more generally which type of rainfall event contributes most to sediment transfer over long timescales (Chen et al., 2015; Reid and Page, 2003). We also found nonlinear scaling between Rt and total landslide area, but without a strong statistical difference between exponential or power-law functions. Exponential functions yield a minimum landsliding amount at low rainfall, that is not physically justified. This apparent contradiction may, however, be resolved by considering a rainfall threshold below which landsliding is null. The higher correlation between Rt and total volume is likely due to the fact that Rt correlates well with maximum landslide size (R2=0.8 with whole landslides, R2=0.9 and almost linear correlation with scar estimates, Fig. 10), with large landslides contributing most of the total volume and erosion. A correlation between Rt and large landslides may arise because landslide stability is determined by the ratio between pore pressure and the total normal stress on the slip plane, meaning that larger landslides that usually have deeper failure planes (Larsen et al., 2010) may only fail with greater precipitation amount. However, given that the trend between total rainfall and the landslide size distribution is much weaker, this correlation may also partly result from a sampling bias as the probability to draw large landslides increases with the total number of landslides. For now, our unreliable estimates of total landslide number do not allow for quantifying this effect.
In any case, several caveats should be taken with the preliminary scalings between total storm rainfall and total landsliding. First, the definition and limit of a single “storm” is not generally agreed in the meteorological community, because the atmospheric fluids suffer perturbations with scale interactions, and therefore with events not independent from each other. Ideally, future studies could categorize storms according to some space-time filtering and analyze the scalings with total landsliding for each storm category. Currently, our database is not sufficient for this. Second, linking total rainfall in a limited area and the total landsliding within the storm footprint implicitly suggests that storm rainfall is somewhat structured with internal correlations between peak rainfall, storm size, and the spatial pattern of rainfall intensity within the storm. This seems to be the case for large tropical storms (Jiang et al., 2008), but should be explored for a broader range of storm types. Orographic effects (Houze, 2012; Taniguchi et al., 2013), focussing high-intensity rainfall on topographic barriers, may also enhance such a correlation between local total rainfall and the broader pattern of rainfall and landsliding. Last, the scaling with rainfall may also be obscured by outliers due to processes not controlled by rainfall. For example, the inclusion of the very long run-out components in several inventories led to larger scattering for both power-law and exponential models and to favor the latter. Therefore, the proposed run-out correction seems essential for future studies. Another issue concerns the normalization of landscape parameters affecting the susceptibility to landsliding, such as hillslope steepness and mechanical strength (Marc et al., 2016; Parise and Jibson, 2000; Schmidt and Montgomery, 1995). Nevertheless, the proportion of flat or submerged land within the area of the most intense rainfall must limit the total landsliding, as it was certainly the case for MI2 or B08 (Fig. 1). Recent, widespread antecedent landsliding may also reduce subsequent susceptibility to rainfall triggered by removing the weak layer of soil or regolith on steep slopes. In the pre-event imagery, we did not see specific evidence of such a limitation, except maybe for J11, where abundant pre-event fresh landsliding were visible near 136,25∘ E/34,29∘ N and 135,9∘ E/34,20∘ and very few new landslides occurred. A more systematic evaluation of this effect may be important when quantitatively comparing the landslide and rainfall patterns. In any case, it is clear that further analysis of this database, possibly extended with additional landslide inventories, should be used by future studies to refine the scaling with rainfall and incorporate the effects of controlling parameters such as available topography, antecedent rainfall or regolith properties (e.g., strength and permeability).
4.2 Relation between rainfall and landslide properties
We found an increase in the proportion of large landslide scars with all storm metrics, but clearest with the total rainstorm (Fig. 7). This is consistent with the idea that large landslides require larger amounts of rainfall to be triggered (Van Asch et al., 1999), as discussed above and exemplified with the strong correlation between Rt and maximal landslide scar (Fig. S10). The large remaining scatter suggests that other differences between the inventories matter, such as differences in the mechanical properties of the substrate (Stark and Guzzetti, 2009). Indeed, broad lithological contrast exists between each event, and sometimes within an event (Fig. S9). The variability in extent and thickness of weak superficial layers (i.e., soils) between the different landscapes affected may also be important. Variations in slope distribution and relief are also wide between each case (Figs. 1, 4) and have also been reported to influence landslide size (Frattini and Crosta, 2013).
We note that the positive correlation between peak rainfall intensity and large landslide abundance is opposed to what could be expected, as more small landslides are expected for pulses of very intense rain leading to the occurrence of transient high pore-water pressure pulses at shallow depth (Iverson, 2000). Given that water retention and hydraulic conductivity may easily change by orders of magnitude between different environments, it may be needed to normalize intensity by the regolith hydraulic conductivity (Iverson, 2000) to understand its potential influence. For the moment, we consider that the correlation between D and I3 and the landslide size distribution exponents likely arises because of the correlation between these storm metrics and Rt (Fig. S4)
In any case, our results suggest that it is not only the landscape properties that set the landslide size distribution but also the trigger characteristics, as previously reported for earthquake-induced landslide size distributions (Marc et al., 2016). This means, for example, that the influence of forcing variability should be assessed and normalized before inverting landslide size distribution parameters to obtain regional variations of mechanical properties (Gallen et al., 2015).
In contrast, aspect ratio or run out did not correlate well with storm metrics and thus obscured any direct correlation between storm metrics and the decay exponents of whole landslide area. This underlines again the importance to isolate scar geometry to deconvolve processes driving landslide initiation and landslide run out. As for the landslide size distribution, landslide run out may likely be influenced by slope and relief distributions, as well as by hydrologic processes. The case of C99, with exceptional run out for most of its landslides is interpreted as the effect of low infiltration rates favoring large runoff generation (Godt and Coe, 2007). This may also explain the abundance of debris flow in other places (C15, J11) but cannot be verified without information on infiltration rate in these places to normalize the intensity variations. An alternative could be to study various storms occurring over the same region, and where infiltration rate or conductivity could be assumed constant; for example, with datasets from multiple typhoons in Taiwan (Chen et al., 2013).
Finally, we observed that most rainfall-induced landslide inventories sample the topographic slope distribution with a minor oversampling beyond the topographic modal slope (Fig. 4). This is in contrast with the case of earthquake-triggered landslides, where we systematically observe preferential landsliding on the steepest slopes (Gorum et al., 2013, 2014; Parise and Jibson, 2000; Fig. 4), quite similar to the case of C99. One-dimensional static force balance shows that the steepest slopes are the most unstable, and therefore the oversampling of steep slopes must be expected if the forcing (pore-water pressure or shaking) is randomly distributed across the whole topography. To obtain equal sampling or undersampling of steep slopes, the forcing intensity must be anti-correlated with slope gradient. Rainfall may be mostly independent of local slopes, but probably not the pore pressure rise that depends on the underground water circulation and thus topography. The pore pressure will thus crucially depend on vertical infiltration and drainage, but also on along-slope contributions. For example, under moderate intensity, but long rainfall, pore-water pressure will reach a higher level in concave, downslope areas (Montgomery and Dietrich, 1994) with a relatively large drainage area, and thus lower slope gradient (Montgomery, 2001). In such a view, landslide slope statistics would bear information on the type of rainfall, short and intense (relative to local permeability) for steep oversampling, while equal sampling and undersampling would relate to moderate and long rainfall. This framework might explain the preferential location on steep slopes observed for the very short duration C99 and possibly C15 (Fig. 4). However, the statistics of C15 are weak, and C99 strong oversampling may mainly relate to specific mass movement triggered by surface runoff such as rilling and the “fire hose effect” (Godt and Coe, 2007). These processes also require high-intensity short-duration events, but also low surficial infiltration rate leading to overland flow able to mobilize relatively loose surface material. For other events, we analyzed the slope-gradient to drainage area relationship for a topography and landslide subset and did not find clear oversampling of high-drainage and gentle-gradient areas in the landslide distribution. A 30 m digital elevation model (DEM) may not be able to accurately resolve the fine-scale pattern of slope gradients and drainage areas on the hillsides, where landslides occur, but it may also suggest that the upslope drainage area is not the main explanation. For example, the subsurface drainage efficiency may also increase with slope gradient, thus making very steep areas less likely to develop large pore pressure and possibly explaining the preferential landsliding of slopes just above the modal slopes for almost all events, independent of rainfall properties. Hydro-mechanical modeling at the catchment scale (von Ruette et al., 2013), applied on several of our dataset may be the only way to test between these different hypotheses. Further constraints on the processes controlling rainfall-induced landslides may also be achieved through a discussion in terms of relative distance from ridge and river (Meunier et al., 2008), as intense and brief storms should yield uniformly distributed landsliding, in contrast to longer, less-intense storms favoring near-river slides.
We present landslide inventories (comprising from a few hundreds to more than 15 000 polygons) associated with eight triggering rain storms from Asia, South America, and North America. We hypothesize that these datasets constitute a global database of rainfall-induced landslides, which allows for studying a number of landslide metrics and their relations to rainfall and landscape properties. Indeed, although spanning a large range of landscape settings, whether in terms of topography, climate, or vegetation, the magnitude of landsliding scales nonlinearly with the magnitude of the storm, here quantified with estimates of the total rainfall. A preliminary analysis indicates that these correlations hold when total rainfall is normalized by long-term monthly rainfall, and how to normalize the storm rainfall by the regional climate should be further investigated. We also found that the correlation between landsliding and rainfall is higher when considering landslide scar estimates obtained through a normalization of landslide run out, as the run-out distribution does not clearly correlate to rainfall. Therefore, after removing the run-out contribution (i.e., focussing on scars) we also find that the landslide size distribution decay exponent seems to be partly controlled by total rainfall, with a greater proportion of large landslides for larger total precipitation. This implies that variations in landslide size distribution cannot be directly interpreted as variations in landscape properties. For total landsliding and maximum local landslide density, power-law scaling based on total rainfall explains 74 % (87 % for total volume) and 76 % (95 % for volume density) of the variance, respectively. Adding a number of other storm events as well as integrating other rainfall forcing parameters or landscape susceptibility properties has, therefore, the potential to yield robust prediction on the magnitude of rainfall-induced landsliding. Finally, we observe that compared to earthquakes, storms tend to trigger landslides that only slightly oversample the topographic slope distribution, possibly due to faster drainage on steep slopes or to underground water accumulation on high-drainage–low-gradient portions of the hillslope. This may bring new, although less straightforward, implications for the difference in resulting topography of bedrock landscape dominated by rainfall-induced or earthquake-induced landslides (Densmore and Hovius, 2000). Although preliminary these insights and scalings show the value of systematically mapping a large sample of the landslides that can be related to a single storm and we identified a number of recent storm events where such a type of inventory could be produced. Although not thoroughly investigated here, a landslide density spatial pattern is likely strongly related to the spatiotemporal pattern of rainfall, and constraining the quantitative links between the two is another challenge that may be addressed with some of the inventories presented here. More generally, the database presented here may also serve as a benchmark for developing and comparing rainfall-induced landslide models, whether empirical, semi- or fully deterministic. These future developments are important challenges in order to understand the natural hazards posed by rainfall-induced landslides as well as their specific implication for the erosion and topographic evolution of landscapes in different climatic settings.
All imagery used to map the landslides are available in public repositories except the images from FORMOSAT-2, GeoEye-1, and aerial photos used for the events in Colorado, Micronesia, and Japan. For the two former, landslide maps are directly available from Godt and Coe (2003) and Harp et al. (2004). For Japan and Brazil, extensive high-resolution imagery is available over most of the areas of interest in Google Earth. The new digitized landslide inventories are available upon request. The hourly rainfall data used in Taiwan and Japan are available in the Supplement, while rainfall data for the other cases are available in the literature. The authors have retrieved the GSMaP_MVK V04 products (Kubota et al., 2006; Ushio et al., 2009) from the “JAXA Global Rainfall Watch” website (https://sharaku.eorc.jaxa.jp/GSMaP/, last access: 29 September 2018). The SRTM-30 m DEM data (NASA JPL, 2013) were retrieved from the online Global Data Explorer, courtesy of the NASA EOSDIS Land Processes Distributed Active Archive Center (LP DAAC), USGS/Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota, (https://gdex.cr.usgs.gov/gdex/, last access: 29 September 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-6-903-2018-supplement.
OM designed the study and performed all analyses with some input from AS, JPM, and MG. TU provided landslide and rainfall data for the J11 event. SHC provided imagery and landslide data for the TW9 event. OM wrote the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
The authors are grateful to the thorough and constructive reviews from Dave Milledge
and an anonymous reviewer that helped to improve and considerably clarify
this manuscript. Odin Marc thanks Patrick Meunier for discussions on
prediction interval and the statistical significance of probability
distribution ratios. This work was carried with the support of the French
space agency (CNES) through the project STREAM-LINE GLIDERS “SaTellite-based
Rainfall Measurement and LandslIde detectioN for Global LandslIDE–Rainfall
Scaling”. Additional support by the open partial agreement “Major Hazards” of
the Council of Europe through the project “Space data in Disaster Risk Reduction:
using satellite precipitation data and hydrological information for
leapfrogging landslide forecasting” was available.
The authors acknowledge the Taiwan Typhoon and Flood Research Institute (National Applied Research Laboratories) and the Japan Meteorological Agency for providing rain gauge data.
Edited by: Michael Krautblatter
Reviewed by: Dave Milledge and one anonymous referee
Ardizzone, F., Basile, G., Cardinali, M., Casagli, N., Conte, S. D., Ventisette, C. D., Fiorucci, F., Garfagnoli, F., Gigli, G., Guzzetti, F., Iovine, G., Mondini, A. C., Moretti, S., Panebianco, M., Raspini, F., Reichenbach, P., Rossi, M., Tanteri, L., and Terranova, O.: Landslide inventory map for the Briga and the Giampilieri catchments, NE Sicily, Italy, J. Maps, 8, 176–180, https://doi.org/10.1080/17445647.2012.694271, 2012. a
Arnone, E., Noto, L. V., Lepore, C., and Bras, R. L.: Physically-based and distributed approach to analyze rainfall-triggered landslides at watershed scale, Geomorphology, 133, 121–131, https://doi.org/10.1016/j.geomorph.2011.03.019, 2011. a, b
Baum, R. L., Godt, J. W., and Savage, W. Z.: Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration, J. Geophys. Res.-Earth, 115, F03013, https://doi.org/10.1029/2009JF001321, 2010. a, b
Blodgett, T. A. and Isacks, B. L.: Landslide Erosion Rate in the Eastern Cordillera of Northern Bolivia, Earth Interact., 11, 1–30, https://doi.org/10.1175/2007EI222.1, 2007. a
Bucknam, R. C., Coe, J. A., Chavarria, M. M., Godt, J. W., Tarr, A. C., Bradley, L.-A., Rafferty, S. A., Hancock, D., Dart, R. L., and Johnson, M. L.: Landslides triggered by Hurricane Mitch in Guatemala – inventory and discussion, USGS Numbered Series 2001-443, https://doi.org/10.3133/ofr01443, 2001. a
Caine, N.: The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows, Geogr. Ann. A, 62, 23–27, https://doi.org/10.2307/520449, 1980. a
Camargo, L. P.: Análise integrada no meio físico dos ribeirões Braço Serafim e Máximo com ênfase nas áreas de fragilidade estrutural, Luís Alves, (SC), PhD thesis, Universidade Federal de Santa Catarina, Florianopolis, available at: https://repositorio.ufsc.br/handle/123456789/157291 (last access: 2 October 2018), 2015. a, b, c
Cannon, S. H., Haller, K. M., Ekstrom, I., Schweig, E. S., Devoli, G., Moore, D. W., Rafferty, S. A., and Tarr, A. C.: Landslide response to Hurricane Mitch rainfall in seven study areas in Nicaragua, USGS Numbered Series 2001-412-A, https://doi.org/10.3133/ofr01412A, 2001. a, b
Cardinali, M., Galli, M., Guzzetti, F., Ardizzone, F., Reichenbach, P., and Bartoccini, P.: Rainfall induced landslides in December 2004 in south-western Umbria, central Italy: types, extent, damage and risk assessment, Nat. Hazards Earth Syst. Sci., 6, 237–260, https://doi.org/10.5194/nhess-6-237-2006, 2006. a
Chang, K.-T., Chiang, S.-H., Chen, Y.-C., and Mondini, A. C.: Modeling the spatial occurrence of shallow landslides triggered by typhoons, Geomorphology, 208, 137–148, https://doi.org/10.1016/j.geomorph.2013.11.020, 2014. a
Chen, Y.-C., Chang, K.-T., Chiu, Y.-J., Lau, S.-M., and Lee, H.-Y.: Quantifying rainfall controls on catchment-scale landslide erosion in Taiwan, Earth Surf. Proc. Land., 38, 372–382, https://doi.org/10.1002/esp.3284, 2013. a, b, c, d, e
Chen, Y.-C., Chang, K.-T., Lee, H.-Y., and Chiang, S.-H.: Average landslide erosion rate at the watershed scale in southern Taiwan estimated from magnitude and frequency of rainfall, Geomorphology, 228, 756–764, https://doi.org/10.1016/j.geomorph.2014.07.022, 2015. a
Clark, K. E., West, A. J., Hilton, R. G., Asner, G. P., Quesada, C. A., Silman, M. R., Saatchi, S. S., Farfan-Rios, W., Martin, R. E., Horwath, A. B., Halladay, K., New, M., and Malhi, Y.: Storm-triggered landslides in the Peruvian Andes and implications for topography, carbon cycles, and biodiversity, Earth Surf. Dynam., 4, 47–70, https://doi.org/10.5194/esurf-4-47-2016, 2016. a
Crone, A. J., Baum, R. L., Lidke, D. J., Sather, D. N., Bradley, L.-A., and Tarr, A. C.: Landslides induced by Hurricane Mitch in El Salvador – an inventory and descriptions of selected features, USGS Numbered Series 2001-444, https://doi.org/10.3133/ofr01444, 2001. a
Dahal, R. K. and Hasegawa, S.: Representative rainfall thresholds for landslides in the Nepal Himalaya, Geomorphology, 100, 429–443, https://doi.org/10.1016/j.geomorph.2008.01.014, 2008. a
Densmore, A. L. and Hovius, N.: Topographic fingerprints of bedrock landslides, Geology, 28, 371–374, https://doi.org/10.1130/0091-7613(2000)28<371:TFOBL>;2.0.CO;2, 2000. a
Domej, G., Bourdeau, C., and Lenti, L.: Mean Landslide Geometries Inferred from a Global Database of Earthquake- and Non-Earthquake-Triggered Landslides, Italian Journal of Engineering Geology and Environment, 87–107, https://doi.org/10.4408/IJEGE.2017-02.O-05, 2017. a
Farr, T. G. and Kobrick, M.: Shuttle radar topography mission produces a wealth of data, Eos, 81, 583–585, https://doi.org/10.1029/EO081i048p00583, 2000.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, D., and Alsdorf, D. E.: The shuttle radar topography mission, Rev. Geophys., 45, n RG2004, https://doi.org/10.1029/2005RG000183, 2007.
Frattini, P. and Crosta, G. B.: The role of material properties and landscape morphology on landslide size distributions, Earth Planet. Sc. Lett., 361, 310–319, https://doi.org/10.1016/j.epsl.2012.10.029, 2013. a, b, c, d
Gabet, E. J., Burbank, D. W., Putkonen, J. K., Pratt-Sitaula, B. A., and Ojha, T.: Rainfall thresholds for landsliding in the Himalayas of Nepal, Geomorphology, 63, 131–143, https://doi.org/10.1016/j.geomorph.2004.03.011, 2004. a, b, c
Gallen, S. F., Clark, M. K., and Godt, J. W.: Coseismic landslides reveal near-surface rock strength in a high-relief, tectonically active setting, Geology, 43, 11–14, https://doi.org/10.1130/G36080.1, 2015. a
Gariano, S. L. and Guzzetti, F.: Landslides in a changing climate, Earth-Sci. Rev., 162, 227–252, https://doi.org/10.1016/j.earscirev.2016.08.011, 2016. a
Godt, J. W. and Coe, J. A.: Map showing alpine debris flows triggered by a July 28, 1999 thunderstorm in the central Front Range of Colorado, USGS Open-File Report, https://doi.org/10.3133/ofr0350, 2003.
Godt, J. W. and Coe, J. A.: Alpine debris flows triggered by a 28 July 1999 thunderstorm in the central Front Range, Colorado, Geomorphology, 84, 80–97, https://doi.org/10.1016/j.geomorph.2006.07.009, 2007. a, b, c, d, e, f, g
Godt, J. W., Baum, R. L., and Chleborad, A. F.: Rainfall characteristics for shallow landsliding in Seattle, Washington, USA, Earth Surf. Proc. Land., 31, 97–110, https://doi.org/10.1002/esp.1237, 2006. a
Gorum, T., van Westen, C. J., Korup, O., van der Meijde, M., Fan, X., and van der Meer, F. D.: Complex rupture mechanism and topography control symmetry of mass-wasting pattern, 2010 Haiti earthquake, Geomorphology, 184, 127–138, https://doi.org/10.1016/j.geomorph.2012.11.027, 2013. a
Gorum, T., Korup, O., van Westen, C. J., van der Meijde, M., Xu, C., and van der Meer, F. D.: Why so few? Landslides triggered by the 2002 Denali earthquake, Alaska, Quaternary Sci. Rev., 95, 80–94, https://doi.org/10.1016/j.quascirev.2014.04.032, 2014. a
Guzzetti, F., Cardinali, M., Reichenbach, P., Cipolla, F., Sebastiani, C., Galli, M., and Salvati, P.: Landslides triggered by the 23 November 2000 rainfall event in the Imperia Province, Western Liguria, Italy, Eng. Geol., 73, 229–245, https://doi.org/10.1016/j.enggeo.2004.01.006, 2004. a
Guzzetti, F., Peruccacci, S., Rossi, M., and Stark, C. P.: The rainfall intensity-duration control of shallow landslides and debris flows: an update, Landslides, 5, 3–17, https://doi.org/10.1007/s10346-007-0112-1, 2008. a, b
Harp, E. and Jibson, R.: Landslides triggered by the 1994 Northridge, California, earthquake, B. Seismol. Soc. Am., 86, S319–S332, 1996. a
Harp, E. L., Hagaman, K. W., Held, M. D., and McKenna, J. P.: Digital inventory of landslides and related deposits in Honduras triggered by Hurricane Mitch, USGS Numbered Series 2002-61, U.S. Geological Survey, Reston, VA, https://doi.org/10.3133/ofr0261, 2002. a
Harp, E. L., Reid, M. E., and Michael, J. A.: Hazard analysis of landslides triggered by Typhoon Chata'an on July 2, 2002, in Chuuk State, Federated States of Micronesia, USGS Numbered Series 2004-1348, https://doi.org/10.3133/ofr20041348, 2004. a, b, c
Houze, R. A.: Orographic effects on precipitating clouds, Rev. Geophys., 50, RG1001, https://doi.org/10.1029/2011RG000365, 2012. a
Hovius, N., Stark, C. P., and Allen, P. A.: Sediment flux from a mountain belt derived by landslide mapping, Geology, 25, 231–234, https://doi.org/10.1130/0091-7613(1997)025<0231:SFFAMB>2.3.CO;2, 1997. a, b, c
Huffman, G. J., Bolvin, D. T., Nelkin, E. J., Wolff, D. B., Adler, R. F., Gu, G., Hong, Y., Bowman, K. P., and Stocker, E. F.: The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales, J. Hydrometeorol., 8, 38–55, https://doi.org/10.1175/JHM560.1, 2007. a
Iverson, R. M.: Landslide triggering by rain infiltration, Water Resour. Res., 36, 1897–1910, https://doi.org/10.1029/2000WR900090, 2000. a, b, c, d
Jiang, H., Halverson, J. B., Simpson, J., and Zipser, E. J.: Hurricane “Rainfall Potential” Derived from Satellite Observations Aids Overland Rainfall Prediction, J. Appl. Meteorol. Clim., 47, 944–959, https://doi.org/10.1175/2007JAMC1619.1, 2008. a, b
Jibson, R. W., Harp, E. L., and Michael, J. A.: A method for producing digital probabilistic seismic landslide hazard maps, Eng. Geol., 58, 271–289, https://doi.org/10.1016/S0013-7952(00)00039-9, 2000. a
Katz, O., Morgan, J. K., Aharonov, E., and Dugan, B.: Controls on the size and geometry of landslides: Insights from discrete element numerical simulations, Geomorphology, 220, 104–113, https://doi.org/10.1016/j.geomorph.2014.05.021, 2014. a
Keefer, D. K., Wilson, R. C., Mark, R. K., Brabb, E. E., Brown, W. M., Ellen, S. D., Harp, E. L., Wieczorek, G. F., Alger, C. S., and Zatkin, R. S.: Real-Time Landslide Warning During Heavy Rainfall, Science, 238, 921–925, https://doi.org/10.1126/science.238.4829.921, 1987. a
Kirschbaum, D., Adler, R., Adler, D., Peters-Lidard, C., and Huffman, G.: Global Distribution of Extreme Precipitation and High-Impact Landslides in 2010 Relative to Previous Years, J. Hydrometeorol., 13, 1536–1551, https://doi.org/10.1175/JHM-D-12-02.1, 2012. a, b
Kirschbaum, D. B., Adler, R., Hong, Y., Hill, S., and Lerner-Lam, A.: A global landslide catalog for hazard applications: method, results, and limitations, Nat. Hazards, 52, 561–575, https://doi.org/10.1007/s11069-009-9401-4, 2009. a
Kubota, T., Shige, S., Hashizume, H., Ushio, T., Aonashi, K., Kachi, M., and Okamoto, K.: Global Precipitation Map using Satelliteborne Microwave Radiometers by the GSMaP Project: Production and Validation, in: 2006 IEEE MicroRad, 290–295, https://doi.org/10.1109/MICRAD.2006.1677106, 2006. a
Lafore, J. P., Stein, J., Asencio, N., Bougeault, P., Ducrocq, V., Duron, J., Fischer, C., Héreil, P., Mascart, P., Masson, V., Pinty, J. P., Redelsperger, J. L., Richard, E., and Arellano, J. V.-G. D.: The Meso-NH Atmospheric Simulation System. Part I: adiabatic formulation and control simulations, Ann. Geophys., 16, 90–109, https://doi.org/10.1007/s00585-997-0090-6, 1997. a
Larsen, I., Montgomery, D., and Korup, O.: Landslide erosion controlled by hillslope material, Nat. Geosci., 3, 247–251, 2010. a, b, c, d
Lehmann, P. and Or, D.: Hydromechanical triggering of landslides: From progressive local failures to mass release, Water Resour. Res., 48, W03535, https://doi.org/10.1029/2011WR010947, 2012. a
Liao, H.-W. and Lee, C.: Landslides triggered by Chi-Chi earthquake, in: Proceedings of the 21st Asian conference on remote sensing, 1, 383–388, 2000. a
Malamud, B. D., Turcotte, D. L., Guzzetti, F., and Reichenbach, P.: Landslide inventories and their statistical properties, Earth Surf. Proc. Land., 29, 687–711, https://doi.org/10.1002/esp.1064, 2004. a, b, c
Marc, O. and Hovius, N.: Amalgamation in landslide maps: effects and automatic detection, Nat. Hazards Earth Syst. Sci., 15, 723–733, https://doi.org/10.5194/nhess-15-723-2015, 2015. a, b
Marc, O., Hovius, N., Meunier, P., Uchida, T., and Hayashi, S.: Transient changes of landslide rates after earthquakes, Geology, 43, 883–886, https://doi.org/10.1130/G36961.1, 2015. a
Marc, O., Hovius, N., Meunier, P., Gorum, T., and Uchida, T.: A seismologically consistent expression for the total area and volume of earthquake-triggered landsliding, J. Geophys. Res.-Earth, 121, 640–663, https://doi.org/10.1002/2015JF003732, 2016. a, b, c, d, e, f
Marc, O., Meunier, P., and Hovius, N.: Prediction of the area affected by earthquake-induced landsliding based on seismological parameters, Nat. Hazards Earth Syst. Sci., 17, 1159–1175, https://doi.org/10.5194/nhess-17-1159-2017, 2017. a, b, c
Meunier, P., Hovius, N., and Haines, A. J.: Regional patterns of earthquake-triggered landslides and their relation to ground motion, Geophys. Res. Lett., 34, L20408, https://doi.org/10.1029/2007GL031337, 2007. a
Meunier, P., Hovius, N., and Haines, J. A.: Topographic site effects and the location of earthquake induced landslides, Earth Planet. Sc. Lett., 275, 221–232, https://doi.org/10.1016/j.epsl.2008.07.020, 2008. a
Meunier, P., Uchida, T., and Hovius, N.: Landslide patterns reveal the sources of large earthquakes, Earth Planet. Sc. Lett., 363, 27–33, https://doi.org/10.1016/j.epsl.2012.12.018, 2013. a
Milledge, D. G., Bellugi, D., McKean, J. A., Densmore, A. L., and Dietrich, W. E.: A multidimensional stability model for predicting shallow landslide size and shape across landscapes, J. Geophys. Res.-Earth, 119, 2014JF003135, https://doi.org/10.1002/2014JF003135, 2014. a
Mondini, A. C.: Measures of Spatial Autocorrelation Changes in Multitemporal SAR Images for Event Landslides Detection, Remote Sensing, 9, 554, https://doi.org/10.3390/rs9060554, 2017. a
Montgomery, D. R.: Slope Distributions, Threshold Hillslopes, and Steady-state Topography, Am. J. Sci., 301, 432–454, https://doi.org/10.2475/ajs.301.4-5.432, 2001. a
Montgomery, D. R. and Dietrich, W. E.: A physically based model for the topographic control on shallow landsliding, Water Resour. Res., 30, 1153–1171, https://doi.org/10.1029/93WR02979, 1994. a, b
NASA JPL: NASA Shuttle Radar Topography Mission Global 1 arc second [Data set], NASA EOSDIS Land Processes DAAC, https://doi.org/10.5067/MEaSUREs/SRTM/SRTMGL1.003, 2013.
Netto, A. L. C., Sato, A. M., Avelar, A. D. S., Vianna, L. G. G., Araújo, I. S., Ferreira, D. L. C., Lima, P. H., Silva, A. P. A., and Silva, R. P.: January 2011: The Extreme Landslide Disaster in Brazil, in: Landslide Science and Practice, Springer, Berlin, Heidelberg, 377–384, https://doi.org/10.1007/978-3-642-31319-6_51, 2013. a, b, c
Nowicki, M. A., Wald, D. J., Hamburger, M. W., Hearne, M., and Thompson, E. M.: Development of a globally applicable model for near real-time prediction of seismically induced landslides, Eng. Geol., 173, 54–65, https://doi.org/10.1016/j.enggeo.2014.02.002, 2014. a
Ono, K., Kazama, S., and Ekkawatpanit, C.: Assessment of rainfall-induced shallow landslides in Phetchabun and Krabi provinces, Thailand, Natural Hazards, 74, 2089–2107, https://doi.org/10.1007/s11069-014-1292-3, 2014. a
Parise, M. and Jibson, R. W.: A seismic landslide susceptibility rating of geologic units based on analysis of characteristics of landslides triggered by the 17 January, 1994 Northridge, California earthquake, Eng. Geol., 58, 251–270, https://doi.org/10.1016/S0013-7952(00)00038-7, 2000. a, b
Petley, D.: Global patterns of loss of life from landslides, Geology, 40, 927–930, https://doi.org/10.1130/G33217.1, 2012. a
Pozzobon, M.: Análise da suscetibilidade a deslizamentos no município de blumenau/sc: uma abordagem probabilística atravées da Aplicação da Técnica pesos de evidência, PhD thesis, Universidade federal do paranã, Curitiba, available at: http://www.floresta.ufpr.br/pos-graduacao/defesas/pdf_dr/2013/t342_0370-D.pdf (last access: 2 October 2018), 2013. a, b
Reid, L. M.: Calculation of average landslide frequency using climatic records, Water Resour. Res., 34, 869–877, https://doi.org/10.1029/97WR02682, 1998. a
Reid, L. M. and Page, M. J.: Magnitude and frequency of landsliding in a large New Zealand catchment, Geomorphology, 49, 71–88, https://doi.org/10.1016/S0169-555X(02)00164-2, 2003. a
Saito, H. and Matsuyama, H.: Catastrophic Landslide Disasters Triggered by Record-Breaking Rainfall in Japan: Their Accurate Detection with Normalized Soil Water Index in the Kii Peninsula for the Year 2011, Sola, 8, 81–84, https://doi.org/10.2151/sola.2012-021, 2012. a
Saito, H., Korup, O., Uchida, T., Hayashi, S., and Oguchi, T.: Rainfall conditions, typhoon frequency, and contemporary landslide erosion in Japan, Geology, 42, 999–1002, https://doi.org/10.1130/G35680.1, 2014. a
Schmidt, K. M. and Montgomery, D. R.: Limits to Relief, Science, 270, 617–620, https://doi.org/10.1126/science.270.5236.617, 1995. a
Stark, C. P. and Guzzetti, F.: Landslide rupture and the probability distribution of mobilized debris volumes, J. Geophys. Res.-Earth, 114, F00A02, https://doi.org/10.1029/2008JF001008, 2009. a, b, c, d
Stark, C. P. and Hovius, N.: The characterization of landslide size distributions, Geophys. Res. Lett., 28, 1091–1094, https://doi.org/10.1029/2000GL008527, 2001. a
Stumpf, A., Lachiche, N., Malet, J.-P., Kerle, N., and Puissant, A.: Active Learning in the Spatial Domain for Remote Sensing Image Classification, IEEE T. Geosci. Remote, 52, 2492–2507, https://doi.org/10.1109/TGRS.2013.2262052, 2014. a
Taniguchi, A., Shige, S., Yamamoto, M. K., Mega, T., Kida, S., Kubota, T., Kachi, M., Ushio, T., and Aonashi, K.: Improvement of High-Resolution Satellite Rainfall Product for Typhoon Morakot (2009) over Taiwan, J. Hydrometeorol., 14, 1859–1871, https://doi.org/10.1175/JHM-D-13-047.1, 2013. a
Tanyaş, H., van Westen, C. J., Allstadt, K. E., Anna Nowicki Jessee, M., Görüm, T., Jibson, R. W., Godt, J. W., Sato, H. P., Schmitt, R. G., Marc, O., and Hovius, N.: Presentation and Analysis of a Worldwide Database of Earthquake-Induced Landslide Inventories, J. Geophys. Res.-Earth, 122, 2017JF004236, https://doi.org/10.1002/2017JF004236, 2017. a
Ushio, T., Sasashige, K., Kubota, T., Shige, S., Okamoto, K., Aonashi, K., Inoue, T., Takahashi, N., Iguchi, T., Kachi, M., Oki, R., Morimoto, T., and Kawasaki, Z.-I.: A Kalman Filter Approach to the Global Satellite Mapping of Precipitation (GSMaP) from Combined Passive Microwave and Infrared Radiometric Data, J. Meteorol. Soc. Jpn., 87A, 137–151, https://doi.org/10.2151/jmsj.87A.137, 2009. a, b
Uchida, T., Tamur, K., and Akiyama, K.: The role of grid cell size, flow routing algolithm and spatial variability of soil depth on shallow landslide prediction, in: 5th International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction and Assessment, 149–157, Italian journal of engineering geology and environment, Padua, Italy, 2011. a
Uchida, T., Sato, T., Mizuno, M., and Okamoto, A.: The role of rainfall magnitude on landslide characteristics triggered by Typhoon Tales, 2011, Civil Engineering Journal, 54, 10–13, 2012 (in Japanese). a
Uchida, T., Okamoto, A., Kanbara, J. I., and Kuramoto, K.: RAINFALL THRESHOLDS FOR DEEP-SEATED RAPID LANDSLIDES, in: International Conference on Vajont 1963-2013/Proceedings – Thoughts and analyses after 50 years since the catastrophic landslide, ITAlian journal of engineering geology and environment, Padua, Italy, 211–217, 2013. a
Van Asch, T. W. J., Buma, J., and Van Beek, L. P. H.: A view on some hydrological triggering systems in landslides, Geomorphology, 30, 25–32, https://doi.org/10.1016/S0169-555X(99)00042-2, 1999. a, b, c, d
von Ruette, J., Lehmann, P., and Or, D.: Rainfall-triggered shallow landslides at catchment scale: Threshold mechanics-based modeling for abruptness and localization, Water Resour. Res., 49, 6266–6285, https://doi.org/10.1002/wrcr.20418, 2013. a, b
Wilson, R. C. and Wieczorek, G. F.: Rainfall Thresholds for the Initiation of Debris Flows at La Honda, California, Environ. Eng. Geosci., I, 11–27, https://doi.org/10.2113/gseegeosci.I.1.11, 1995. a
Yagi, H., Sato, G., Higaki, D., Yamamoto, M., and Yamasaki, T.: Distribution and characteristics of landslides induced by the Iwate-Miyagi Nairiku Earthquake in 2008 in Tohoku District, Northeast Japan, Landslides, 6, 335–344, 2009. a





