the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A versatile, linear complexity algorithm for flow routing in topographies with depressions
Guillaume Cordonnier
Benoît Bovy
Jean Braun
We present a new algorithm for solving the common problem of flow trapped in closed depressions within digital elevation models, as encountered in many applications relying on flow routing. Unlike other approaches (e.g., the Priority-Flood depression filling algorithm), this solution is based on the explicit computation of the flow paths both within and across the depressions through the construction of a graph connecting together all adjacent drainage basins. Although this represents many operations, a linear time complexity can be reached for the whole computation, making it very efficient. Compared to the most optimized solutions proposed so far, we show that this algorithm of flow path enforcement yields the best performance when used in landscape evolution models. In addition to its efficiency, our proposed method also has the advantage of letting the user choose among different strategies of flow path enforcement within the depressions (i.e., filling vs. carving). Furthermore, the computed graph of basins is a generic structure that has the potential to be reused for solving other problems as well, such as the simulation of erosion. This sequential algorithm may be helpful for those who need to, e.g., process digital elevation models of moderate size on single computers or run batches of simulations as part of an inference study.
- Article
(3728 KB) - Full-text XML
- BibTeX
- EndNote
Finding flow paths on a topographic surface represented as a digital elevation model (DEM) is a very common task that is required by many applications in domains such as hydrology, geomorphometry, soil erosion, and landscape evolution modeling, and for which various algorithms have been proposed for either gridded DEMs (e.g., O'Callaghan and Mark, 1984; Jenson and Domingue, 1988; Quinn et al., 1991; Tarboton, 1997) or unstructured meshes (e.g., Jones et al., 1990; Banninger, 2007).
Closed depressions may arise in DEMs because they are real topographic features or result from interpolation error during DEM generation or its lack of resolution. These spurious local minima need to be resolved because they disrupt flow routing, produce hydrologically unrealistic results, or introduce artificial singularities that may result from a sudden, unrealistic jump in computing discharge. Flow routing is often corrected by filling depressions (e.g., Jenson and Domingue, 1988), carving channels through artificial sills (Rieger, 1998), or by using hybrid breaching-filling techniques (Lindsay, 2016).
Although not having a linear time complexity, the most recent algorithms of depression removal – e.g., the Priority-Flood algorithm and its variants (Barnes et al., 2014a; Zhou et al., 2016; Wei et al., 2018) – have been optimized so that they can be used efficiently on large datasets. To increase performance for very large datasets, further optimization efforts have been focused primarily on rather complex, parallel variants of these algorithms (Barnes, 2016; Zhou et al., 2017).
Yet, in some applications flow path enforcement still remains the main bottleneck. This is for example the case in many landscape evolution models (LEMs) simulating an evolving topography (see Tucker and Hancock, 2010, for a review) and that rely on flow routing to compute erosion rates. To produce realistic results, flow path enforcement is often applied many times, i.e., at each simulation time step (Fig. 1), even when this eventually becomes irrelevant as the modeled erosional processes usually tend to remove depressions rather than deepen or add new ones (Braun and Willett, 2013). Furthermore, LEMs are also used as forward models in sensitivity analyses and/or inferences on the parameters that control erosional processes, which often require running a large number of models to adequately explore the parameter space. Parallel flow routing and hydrological correction algorithms do not help much here, as grid-search and/or sampling methods (e.g., Sambridge, 1999) are generally easier to implement and more effective to execute in parallel. Highly optimized, sequential algorithms are still needed in this case.
We have developed a new method of flow enforcement that is based on the explicit building of a graph of drainage basins (possibly encompassing depressions) and the computation of the flow paths both within and across those basins. This idea was first introduced in a Computer Graphics implementation of the stream power law (Cordonnier et al., 2016), but with a sub-optimal complexity. Although this approach may appear naive at first glance, we have improved it by using fast algorithms of linear complexity at each step of the procedure, which now makes the whole computation very efficient. Not only does this method enable the use of a wide range of techniques of flow enforcement within the closed depressions (e.g., depression filling, channel carving, or more advanced techniques), but it also provides generic data structures that could potentially be reused for solving other problems like modeling the behavior of erosion–deposition processes within those depressions.

Figure 1 Simulation of the evolution of an escarpment over 70 time steps of 1000 years each and on a 1024×256 regular grid, using the FastScape model (Braun and Willett, 2013, see also Sect. 3 below). The grid nodes of the leftmost column (boundary nodes) have a fixed elevation while the initial elevation of the other nodes corresponds to a 500 m high flat surface with small random perturbations. Using the same set of model parameters, simulation results are shown (a) without and (b) with correction of flow routing in local depressions at each time step. As illustrated, flow path disruptions in (a) cause a much slower migration of the escarpment, while the topography predicted in (b) is usually considered more realistic, especially under temperate or humid climates.
After a detailed presentation of the different steps of the method, we will show in the sections below through some results how our algorithm behaves and performs compared to existing solutions of flow path enforcement. We will finally discuss the assets and limitations of our method, with some focus on landscape evolution modeling applications.
The input of the algorithm is a topography , where 𝒩 is a set of nodes and ℰ is a set of edges that link pairs of neighbor nodes. A node n is given a horizontal position pn and a vertical elevation zn. A topography may for example result from a triangulation or correspond to a regular grid of four-connectivity (i.e, four neighbors per nodes) or eight-connectivity (i.e., also including diagonal neighbors). We follow the conventions of Braun and Willett (2013) to define flow paths on the topography: each node n is given (1) a single flow receiver, rcv(n), which corresponds to that of its (strictly) downslope neighbors having the steepest slope, and (2) a set of flow donors, Donors(n), which is a subset of the neighbors of n and is defined as . We set rcv(n)=∅ when n is a singular node: it corresponds to either a user-defined boundary node (e.g., a node on the domain boundary) or a local minimum in the topography, i.e., a node inside the domain where all of its neighbors have a higher elevation, and correspond to either a pit or a flat-bottomed depression in Lindsay (2016) terminology.
We propose an algorithm that updates the receivers of a subset of 𝒩 such that the flow is never trapped in local minima. This algorithm primarily aims at resolving local minima in the context of flow routing and thus leaves the elevation of the nodes unchanged. Hence it breaks the previously introduced definition of a flow receiver: the new receivers assigned by the algorithm generally produce some localized “upslope flow”. While this seems unnatural and may not be wanted, the data structures used by the algorithm provide enough information to efficiently address this issue later depending on the application, which is beyond the scope of this work. Still, the algorithm ensures that the updated flow routing stays consistent across the whole topography by respecting the following properties for each node n of the topography.
-
There exists a single boundary node b (not a local minimum), and a unique flow path from n to b. The flow path is defined as the set of nodes rcv(n), .
-
This flow path does not contain any cycle; i.e., each node appears only once in P.
-
The receivers defining P are chosen such that it satisfies properties 1 and 2, and minimizes the energy E, defined as
As a first approximation, we set Ei=zi (the altitude of the node). We will discuss later the special case of nodes under water level.
Our method is essentially based on the computation of a graph connecting adjacent drainage basins. We define a basin as the set of all nodes that flow toward the same singular node (Fig. 2b). A basin is either a boundary basin or an inner basin depending on whether the singular node is a boundary node or a local minimum.
To better explain the problem that we want to solve, we consider a filled topography as the result of an ideal physical process where a perfectly fluid material has been poured onto an impermeable ground and stabilized at steady state. For a node n, we define as water level (wn) the elevation of the fluid surface, and as a spill any node s such that and zs>wrcv(s). Note that for a flow routing observing the aforementioned properties, the water level can be computed as . We also use the term depression from Lindsay (2016) terminology, and we define it with respect to a basin B as a subset of nodes of B under water level, characterized by wn=wrcv(n). Note that the water level of a boundary basin corresponds to the elevation of its associated boundary node so that it contains no depression. In the case of nested depressions, the water level of a basin may be higher than the elevations of all its nodes, which means that the spill does not always belong to B.
The energy of the nodes should be changed to Ei=wi, but as described later, one may choose various routing strategies inside the depressions depending on the application. Therefore, we allow any path within depressions by setting Ei to zero inside them, and keeping Ei=zi elsewhere.
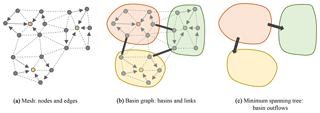
Figure 2 Illustration of the inputs and the first steps of the proposed flow routing algorithm. (a) The input topography is defined on top of a mesh by a set of nodes and edges. A single edge is selected for each node, it connects the node to its flow receiver, i.e., its neighbor with the steepest slope. Nodes with no receiver are local minima (colored in the figure). (b) All the nodes that flow to a same local minimum belong to the same basin. A graph of basins is created by connecting together adjacent basins with links, which are materialized on the mesh by edges representing the passes, i.e., the crossings of lowest elevation that connect each pair of basins (black thick arrows). (c) Some of the links are selected by computing a minimum spanning tree and the corresponding passes are oriented in the direction of the flow across the basins (unidirectional arrows). This structure is then used to update the flow receivers so that the flow reaches the domain boundaries without being interrupted.
One may break the problem of flow path enforcement down to three smaller problems: find the spill of each depression, force the flow within the depressions to be routed toward their respective spill, and ensure that the flow through the spills is properly routed into adjacent basins. The proposed algorithm addresses this problem in an explicit manner and can be divided into three main stages.
-
Compute the basins and link all pairs of adjacent basins (Fig. 2b).
-
Select only some of the basin links computed at the previous stage and orient them such that the flow is routed consistently across adjacent basins, from inner basins toward the boundary basins (Fig. 2c). This operation is not trivial: an optimal selection needs a global knowledge of the whole basin graph. To do so, we use an algorithmic structure: a minimum spanning tree of the basin graph. We propose here two algorithms, a simple one with O(nlog n) complexity, and a more complex one with O(n) complexity.
-
Update the flow receivers. Using the links selected at the previous stage, we update (only some of) the receivers to enforce the flow both within and across inner basins so that it is ensured to finally reach the boundary basins and their associated boundary nodes. We propose three different methods (one may choose a method over another depending on the specific problem to solve).
Each of these stages processes the whole DEM, and as such are run only once for a given topography. They are each detailed in the next sections.
2.1 Basin computation and linkage
This first stage consists in first assigning a basin identifier, basin_id(n), to each node n of the topography. The identifiers are added sequentially by starting at singular nodes and parsing the nodes using a depth-first traversal in the direction of the donors (see Appendix A1). The case of flat-bottomed depressions does not require any particular treatment: all nodes within flat areas are singular nodes and therefore are each assigned a unique basin identifier.
Then, the links connecting all pairs of adjacent basins are retrieved. To each link also corresponds an edge of the topography, here called a pass, which represents the crossing of lowest elevation between the two basins. For example, the link connects the basins B1 and B2 and has the corresponding , where n1∈B1 and n2∈B2 and where the chosen (n1,n2) minimizes . We define a single procedure to retrieve both the links and their pass (see Appendix A2). This procedure parses each edge of the topography: if the two nodes of the current edge each have different basin identifiers, then (1) it adds a new link if no link has been already set for these two basins, and (2) it sets or maybe updates the pass of that link with the current edge.
The sets of basins ℬ and the set of retrieved links ℒ both define a basin graph. It is worth noting that, at this stage, the links and passes are not oriented and that only one link and pass are stored for two adjacent basins. The procedure described above runs sequentially and will not add the link (B2,B1) if it already added the link (B1,B2).
2.2 Flow routing across adjacent basins
This second stage tackles the problem of selecting the right subset of links so that we obtain consistent flow paths on the basin graph. To illustrate the proposed solution, let us start from an inner basin. If it is filled with water, the water level will rise until it finds a pass where water eventually pours into another, adjacent basin. The associated link is then called the outflow of the basin. Hence, routing the flow across the basins consists in connecting all outflows such that the resulting flow paths, from inner basins to the boundary basins, have the same properties as stated above; i.e., those paths are unique, contain no cycle, and minimize the energy needed to reach the boundary basins.
If we add to the basin graph a virtual basin (let us call it external basin) to which we link all the boundary basins (i.e., the external basin may be viewed as a bucket collecting all the flow that leaves the domain), then we can represent the connected outflows using a specific algorithmic structure: a tree. More specifically, a basin tree is a tree that satisfies the properties above: it actually corresponds to a minimum spanning tree of the basin graph, i.e., a subset of the basin graph resulting from a selection of the links so that the following energy is minimized:
where 𝒪 is the set of selected links (or the set of outflows) and zpass(L) is the elevation of their respective passes.
We propose two algorithms for the computation of a minimum spanning tree. Kruskal's algorithm is very generic and simple with a log-linear complexity. We also propose a second algorithm, which leverages the planar nature of the basin graph to reach a linear complexity.

2.2.1 Kruskal's algorithm
Kruskal's algorithm (Kruskal, 1956) is one of the most classical algorithms used for computing minimum spanning trees and is known to have a O(mlog m) complexity, where m is the number of links. The number of links being always bounded by a linear function of the number n of nodes in the grid (Euler formula), using this algorithm induces a global upper bound of O(nlog n) on the complexity of our solution. This algorithm uses a union–find structure to store and merge equivalence classes of objects (see Algorithm 1). The idea here is to parse all links L∈ℒ sorted by increasing elevation zpass(L), progressively grouping each pair of basins as a larger, virtual one (equivalence class). All subsequent paths between basins within this equivalence class are discarded to prevent loops. The union–find data structure has three operations:
- MakeSet
-
Create an equivalence class containing a single element.
- Union
-
Merge two equivalence classes.
- Find
-
Get the equivalence class of an object.
The optimal implementation of the union–find structure provides a 𝒪(α(N)) complexity for these operations, where N is the number of elements in the structure (i.e., here the number of basins) and α is the inverse Ackermann function whose complexity is lower than O(log N). This however requires first sorting the links by increasing weight (i.e., by the elevation of their respective passes), which finally yields a O(mlog m) complexity for the whole computation.
2.2.2 Planar graphs
The problem of finding the minimum spanning tree is known to have a O(N) complexity when the graph is planar (Mareš, 2002). A planar graph is a graph which can be embedded in a plane such that none of its edges cross another one. The basin graph described in Sect. 2.1 is an example of a planar graph. The key intuition behind the algorithm proposed in Mareš (2002) is that at least half of the vertices of a planar graph have at most eight neighbors. The algorithm is then an adaptation of another classical algorithm, named Boruvka's algorithm (Boruvka, 1926); see Algorithm 2 for more details. The O(N) complexity comes from the fact that at each step of the outer loop, we parse and remove at least half of the nodes of the graph, and . As the number of grid nodes n>N, the complexity of this algorithm is bounded by O(n). As demonstrated by Mareš (2002), the limit of eight neighbors for the selection of a basin in the inner loop is critical in halving the number of edges at each iteration of the outer loop and thus in obtaining a linear time complexity.

A special case may arise when the basin graph is computed from a grid of eight-connectivity. In this case, the edges of the graph may cross each other due to the diagonal connectivity, possibly making the basin graph not perfectly planar. This is, however, rather unlikely as it implies that two passes connecting different basins are found on the two diagonals connecting four adjacent nodes of the grid. Furthermore, this issue does not impact the correctness of the algorithm. Only the linear complexity is not formally proven. Because it is not planar, the case of an eight-connectivity grid would fall in the second category mentioned by Mareš (2002) of graphs closed on graph minor. We have validated this experimentally by randomly computing minors of differently sized eight-connected graphs. We found an edge density of 4, implying that half of the basins in the basin graph are linked to at most 16 adjacent basins (and not eight as for planar graphs) at any step of the algorithm. Therefore, we have demonstrated the linear complexity for eight-connected graphs experimentally, although future work is needed to prove this in a formal framework.
2.3 Updating flow receivers
The basin tree obtained at the previous stage must be oriented before routing the flow from inner basins to the boundary basins. This is achieved by traversing the tree in the reverse order (i.e., starting from the boundary basins) and labeling the two nodes of each pass, one as nin (incoming flow) and the other one as nout (outgoing flow). Depending on their elevation, either nin or nout is the spill node of the corresponding basin.
The last stage then consists in updating the flow receivers so that any flow entering an inner basin is ensured to leave the basin through nout. The most straightforward solution would be to only update the receiver of each local minimum p so that rcv(p)=nout. Note that if nin has a higher elevation than nout, then two receivers must be updated: rcv(nin)=nout and rcv(n)=nin. This very simple solution ensures topological continuity of the flow but does not preserve its spatial continuity. We therefore propose two other, more realistic methods: one similar to depression filling and another similar to depression carving. Note that we use carving and filling as metaphors as our algorithm only changes the flow graph connectivity without altering elevation values. For each of the variants, the donors and stack structures need to be updated to reflect the changes in the receivers.
2.3.1 Depression carving
The idea here is to mimic the effect of a river carving a narrow trench between the bottom of the depression and the spill: a new, single path is computed from the local minimum to the pass. In fact, the most direct path is already defined by the flow receivers that were computed initially, but it is in the reverse order, i.e., from the pass to the local minimum. Hence, it is trivial to follow this path and progressively revert the receivers until the local minimum is reached (see Algorithm 3).

2.3.2 Depression filling
Unlike the previous method, we update here the receivers as if the depressions were completely filled by some material. We define a procedure that starts at a pass and then progressively parses all neighbor nodes in a breadth-first order as long as these are below water level, at the same time updating the receiver of the current parsed node as being one among its neighbors that has already been parsed (see Algorithm 4). We repeat this procedure for all depressions by traversing the basin tree from the boundary basins to the most inner ones so that accurate water level values can be computed during the procedure. Receivers are chosen according to a cost function that we define here as the minimal Euclidean distance between a node and nout. This function does not yield the perfect path patterns that one would obtain by including obstacles in the computation of the Euclidean distance on a regular grid, but it is simple and efficient while being accurate enough. We prefer this method over a simple breadth-first search, which depends on the order in which neighbors are visited and which leads to more pronounced straight lines after erosion, due to the four- or eight-connectivity.

Our algorithm is run under different settings to illustrate its behavior and compare it with some other state-of-the-art methods. Most of the examples below are shown within the context of landscape evolution modeling, using a simple model of block uplift vs. channel erosion by the stream power law. This model simulates the evolution of the topographic surface z, which can be written as follows:
where U is the uplift rate, A is the drainage area (a surrogate for water discharge), ∇z the local topographic gradient, and K, m, and n are the parameters of the stream power law. The latter is solved numerically on a 2-D regular grid using an implicit scheme of linear complexity (see the FastScape algorithm described in Braun and Willett, 2013). In particular, the local gradient ∇z is chosen as the slope between the eroded node and its receiver (forced to 0 if its value is negative in order to avoid erosion artifacts in the case of “upslope flow” caused by updated receivers). We choose this algorithm which is particularly well suited to our flow routing method, although some discussion on the limits of this algorithm can be found in Campforts and Govers (2015) for steep topography. As common settings, we use , m=0.4, and n=1. Grid spacing is 100 m in both directions.

Figure 3Our algorithm of flow enforcement run on a synthetic case. (a) Hillshade and contour plot of the input topography with apparent depressions. (b) Basins (areas of unique, random colors) and all passes connecting adjacent basins (thin black lines). (c) Flow directions across the basins (white arrows), as resulting from the computation of a minimum spanning tree from the basin graph, and water level (blue areas) after some erosion is applied to the input topography.
3.1 Illustration of the algorithm
The behavior of our algorithm of flow path enforcement is best illustrated using a simple synthetic topography as input. A set of 25 local minima is sampled on a regular grid of 500×500 nodes and the elevation of the topographic surface is locally computed as a fixed proportion of the distance to the nearest local minimum (Fig. 3a). The first step of the algorithm delineates the basin of each local minimum and finds all possible connections (links) between the basins, located at the lowest pass between each pair of adjacent basins (Fig. 3b). Then, a minimum spanning tree is computed from the graph of these links to find the path of minimum energy that would allow the water to leave the basins (white arrows in Fig. 3c). The flow receivers can then be updated by using the edges of this basin tree. The updated receivers are in turn used by the FastScape algorithm to slightly erode the basin boundaries during one time step of 100 years. The result is shown as well as the final water level in Fig. 3c.
3.2 Effect of flow path enforcement strategies on eroded topographies

Figure 4Demonstration of the effect of flow path enforcement on erosion, using different strategies of flow receivers “correction” within inner basins. (a) Hillshade and contour plot of the initial topography. (b), (c) and (d) Hillshade and contour plot of the topography obtained after running a single time step of 5000 years with channel erosion only (no uplift), with flow receivers updated using each of the different strategies described in Sect. 2.3. Water level is shown in blue, and is computed by propagating the spill elevation while parsing the nodes in the upstream order (based on updated donors).
Figure 1 already shows the effect of flow path enforcement vs. no enforcement on the evolution of an escarpment under active erosion processes. A second set of experiments, shown in Fig. 4, illustrates the impact that the different strategies of flow receiver updating have on the evolution of the topographic surface under the action of channel erosion. The input synthetic topography is defined on a 100×100 regular grid and looks like an inverted pyramid with 45∘ regular slopes, forming a single, big depression (Fig. 4a). The node at the middle of the top boundary is the only node that is not part of the depression: it has the same elevation as the node at the center of the grid and it is defined as a boundary node. A single time step of 5000 years of erosion only (no uplift) is performed using each of the strategies described in Sect. 2.3.
- Simple correction.
-
In this specific case, the algorithm updates the receivers of only three nodes: (1) one of the neighbors of the boundary node, which here corresponds to the spill of the closed depression, (2) one of the neighbors of the spill that, together with the spill, forms the pass connecting the depression to the boundary node, and (3) the local minimum at the bottom of the depression. The new assigned receivers are for (1) the boundary node itself, (2) the spill, and (3) the other node of the pass. We can see in Fig. 4b that this strategy does not allow channel erosion to propagate much from the boundary node into the closed depression. In fact, drainage area values close to the boundary node are high enough to trigger erosion but the low values of drainage area in the vicinity (within the depression) prevent further propagation of the erosion wave.
- Depression carving.
-
Unlike the former strategy and as expected, Fig. 4c shows that the depression carving strategy allows erosion to propagate toward the local minimum along a narrow and deep trench.
- Depression filling.
-
Using the depression filling strategy, flow receivers are updated over a large area of the depression as if the water surface was replaced by a very gentle slope toward the spill. As a result, erosion affects a great part of the modeled domain, with the emergence of a star-like pattern centered at the spill (Fig. 4d). The number and disposition of the branches of the star are due to the grid eight-connectivity used here.
Choosing one strategy over another greatly depends on the specific application. For example, the simple correction strategy may be acceptable if one assumes that no erosion could happen in depressions below the water level. However, interrupted drainage area patterns within the depressions may be problematic when used with erosion algorithms like the FastScape model, which uses an implicit time scheme for solving the stream power law but still treats drainage area explicitly, resulting in too slow opening of the closed depressions by erosion. The depression carving or depression filling strategies generally yield better results in the latter case. These two strategies have, however, contrasting behaviors and choosing one or the other will depend on several criteria such as the size (i.e., depth vs. volume) of the depressions.
3.3 Performances
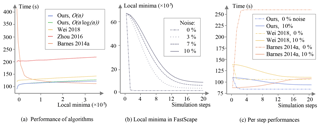
Figure 5Results from benchmarks assessing the performance of our algorithm for local minima resolution – including both O(nlog n) Kruskal's and O(n) Mareš' variants for computing the minimum spanning tree, compared to three other solutions based on variants of the Priority-Flood depression filling algorithm proposed by Barnes et al. (2014a), Zhou et al. (2016), and Wei et al. (2018). See text for more details about the setup of these benchmarks. (a) Execution time measured for local minima resolution applied once to a synthetic input topography vs. total number of local minima generated in the input topography. (b) Evolution of the number of local minima detected in the topography obtained at each of the first 20 time steps of a FastScape model run. Each curve corresponds to a given magnitude of random perturbations added to produce spatially variable uplift rates (magnitude values are relative to a fixed uplift rate of ). (c) Execution time measured for local minima resolution at each time step, with either spatially uniform or variable uplift rates (i.e., a relative noise magnitude of either 0 % or 20 %). The blue curves refer to our algorithm using the O(n) variant for computing the minimum spanning tree.
To assess the performance of our algorithm, we have run multiple benchmarks under various settings. Although these benchmarks mostly take place in the framework of landscape evolution modeling, they provide results that may be useful in other applications too. Note that for better readability, we present here only the results from benchmarks applied to a fixed grid of 16 384×16 384 nodes. We obtain consistent results for other grid sizes.
We have run benchmarks for our algorithm – including the two variants for computing the minimum spanning tree but considering only the depression filling strategy – as well as for three other state-of-the-art algorithms of local minima resolution, respectively proposed by Barnes et al. (2014a), Zhou et al. (2016), and Wei et al. (2018). All three of those algorithms fill the depressions using improved variants of the Priority-Flood algorithm that reduce the number of nodes processed by a priority queue. The Barnes et al. (2014a) variant used here, i.e., Priority-Flood+ϵ, is only slightly optimized but has the advantage of filling the depressions with a nearly flat surface so that flow directions can be determined. Interestingly, the simplicity of this first version makes it the most efficient when the number of local minima is large (see Sect. 4). While being the most optimized sequential variant that has been proposed so far, the Wei et al. (2018) variant fills the depressions with perfectly flat surfaces and thus has to be combined with a flat resolution algorithm – we use here an optimal O(n) algorithm proposed by Barnes et al. (2014b). We apply the same treatment to the Zhou et al. (2016) variant. All variants fill the depressions by directly updating the elevation values on the grid. To ensure proper comparison with our algorithm, we thus need to run them on a temporary copy of the elevation values before computing the flow receiver for each node of the grid. With our algorithm being optimized for a sequential usage, we chose not to compare it to the parallel versions of Barnes (2016) and Zhou et al. (2017). Both the algorithms and the benchmarks are implemented using the C++ language. For the state-of-the-art algorithms, we reuse the implementations available in the RichDEM library v2.2.9 (Barnes, 2018). The benchmarks where computed on an Intel Xeon Silver 4110 CPU (2.1 GHz, 32.0 Go RAM). We used Microsoft Visual Studio compiler with fast optimization options. Note that because of the differences in the design/implementation used in RichDEM vs. our code, the benchmarks presented here should be seen as an illustration of the theoretical complexities of the algorithm variants rather than a strict comparison of their actual performances.
In a first set of benchmarks, we create an input topography by running the FastScape model (starting from an initial flat surface with small random perturbations) until steady state is reached (the uplift rate is set to ), and then by lowering the elevation of an arbitrary number of nodes down to 10−5 m below their lowest neighbors. Those nodes are chosen randomly on even rows and columns to make sure that we obtain the same number of local minima in the input topography. Note that each generated basin has a size of at most nine cells, which allows for a fine control on the cumulative size of the depressions. Figure 5a shows the execution times of our algorithm vs. state-of-the-art algorithms for an increasing number of local minima. We can see that in these settings our algorithm (both variants for the computation of the minimum spanning tree) globally outperforms the state-of-the-art solution of Wei et al. (2018) combined with flat resolution. Note that without combining it with a flat resolution algorithm, the Wei et al. (2018) algorithm shows an equivalent performance to our approach, provided that the depressions remain evenly distributed. In that case, the main difference between the two approaches is that ours provides data structures (flow paths, basin graph) that might be reused elsewhere. By contrast, the Barnes et al. (2014a) Priority-Flood variant shows an inverse trend: it performs much worse in the absence of depression but the execution time rapidly decreases when increasing the total number of local minima, eventually achieving better performance than our algorithm. This is explained by the very simple implementation of this variant, in which all the nodes are processed by a priority queue in the absence of depression (not optimal) while a plain queue is used for most of the nodes if the topography is largely covered by depressions, making this variant near optimal in that specific case. Note that for high numbers of local minima we also start to discern in Fig. 5a the difference in performance of the variants used to compute the minimum spanning tree, here explained by their log-linear vs. linear complexity.
In a second set of benchmarks, we analyze the performances of the algorithms for local minima resolution through full simulations of landscape evolution. We run the FastScape model over 20 time steps of 10 000 years each, starting from a flat topography with small random perturbations (thus containing many local minima) and using fixed boundary conditions, i.e., boundary nodes all along the grid boundaries. The simulations are all based on a uniform uplift rate of but each differ by the magnitude of the random field (created on a coarser, 1500×1500 grid) added to produce spatially variable uplift rates. This magnitude ranges from 0 % to 20 % of the uniform uplift rate. As shown in Fig. 5b, a greater magnitude of perturbation of uplift rates reduces the rate at which the local minima disappear under the action of channel erosion as the simulation proceeds. With no perturbation, all local minima are removed after the first time step. This has important implications for the overall time spent on resolving local minima during a simulation. Figure 5c shows that, with uniform uplift, our algorithm greatly optimizes this overall time compared to the Priority-Flood variant of Barnes et al. (2014a). Even with variable uplift rates, our algorithm performs better after only a few time steps.
We focus our discussion on an in-depth analysis of the differences in performance obtained by the different state-of-the-art algorithms, as reported in the section above. Barnes et al. (2014a) propose progressively flooding the topography from exterior to interior, keeping in a priority queue all the parsed nodes except for the ones in depressions, which are processed using a plain queue. The operations used in this algorithm can be split in two main categories: one handling the nd nodes in depression areas, with nd<n the total number of nodes, and another one handling the other “regular” nodes, , using the priority queue. As a depression encloses at least one node (a local minimum) and zero or more nodes in the immediate vicinity, the total number of nodes in depression areas is always greater than or equal to the total number of local minima nl, that is, . Therefore, the complexity of Barnes et al. (2014a) Priority-Flood variant is bounded by , where k0, k1, and k2 are constants. Due to the very simple formulation of this algorithm, k1 is very small. The improved variants of Priority-Flood proposed by Zhou et al. (2016) and Wei et al. (2018) further reduce the number of nodes that are processed by the priority queue by carefully selecting spill candidates among the regular nodes. In those variants, the total number of nodes processed by the priority queue becomes nearly proportional to the number of local minima, inverting the formulation of the complexity that is here bounded by . Because those variants are more complex, k4 has higher values.
We also derive the complexity of our algorithm taking its stages separately. The first and last stages, i.e., the computation of the basin graph and the update of flow receivers, are both bounded by k6+k7n, with a relatively high value for the k6 and k7 constants. The second stage, i.e., the computation of the minimum spanning tree, is bounded by either k8 nl log nl when using the Kruskal's algorithm or k9 nl when using the algorithm proposed by Mareš (2002), with k8<k9. Both expressions above are valid considering that nl∼N values (the number of basins) for N large.
The complexities of the algorithms that we have derived here are all consistent with the benchmark results shown in Fig. 5a. The difference between the two minimum spanning tree algorithms is visible only for a large number of local minima, as predicted by their respective asymptotic complexity, while being unnoticeable for low nl where the other stages of the processing prevail. Similar expressions obtained for the complexity of our algorithm vs. the solution based on Wei et al. (2018) are also well illustrated by sub-parallel curves in the figure. The inverse trend observed for the Barnes et al. (2014a) solution is explained by its complexity, where the term tends towards zero as nl increases.
For all the algorithms compared here, the memory consumption grows linearly with the DEM size. Barnes et al. (2014a), Zhou et al. (2016), and Wei et al. (2018) Priority-Flood variants only use a supplementary queue to unload the priority queue, making it very memory-efficient. By contrast, our algorithm stores more information like the structures used for representing flow paths (receivers, donors, and stack), the basin graph, and possibly some additional data structures like those needed by the algorithm of Mareš (2002). Some of these data might be required for further processing, e.g., the flow paths in landscape evolution modeling applications. Other data related to the basin graph increase the memory consumption, although in practice the number of local depressions – and thus the size of the graph – is small enough with respect to the size of the grid, resulting in only a small memory overhead compared to the Priority-Flood variants.
We have presented here a new algorithm for flow path enforcement in topographies with depressions. We have designed this algorithm within the framework of landscape evolution modeling and we have demonstrated through benchmarks that, in this scope, it may greatly improve performance compared to other state-of-the-art solutions. The potential of this algorithm is, however, not limited to landscape evolution models. On a broader scope, the basin graph and its minimum spanning tree are generic structures that other applications may leverage, possibly through derived quantities such as the water level of each depression. We propose here optimal methods to compute those structures and quantities. Despite the fact that our algorithm is rather complex and requires some work to be properly implemented, it is designed in a composable way such that it is easy to reuse one or several of its components. Adding new features like alternative strategies of flow path enforcement within the depressions would require only little effort, too.
While being versatile, this new algorithm does not provide a universal solution to the problem of flow routing both within and across closed depressions. Perhaps its main limitation is the assumption of single- direction flow, i.e., each node has one unique flow receiver. Adding full support for multiple-direction flow (MDF) without losing in performance is rather difficult and would require a fair amount of redesign work at each of the three stages of the algorithm:
-
Basin computation should take into account divergent flow (basin labels are not unique for grid nodes located on drainage divides).
-
It should be theoretically possible to route the outflow from an inner basin into more than one of its adjacent basins (this is currently not possible using a minimum spanning tree computed from the basin graph).
-
Alternative, MDF-compliant methods should be implemented to update the flow receivers within the depressions.
Other algorithms like the Priority-Flood do not have that limitation: they act directly on elevation values and do not prevent us from applying MDF flow routing methods on the modified topography.
Another limitation of this algorithm is its sequential implementation. Further work is needed to adapt it so that it could be run on modern, multi-core, and/or GPU-based architectures. Still, many use cases would benefit from the current implementation. These include processing datasets of moderate size on a single computer or running batches of simulations or analysis pipelines, e.g., in the context of sensitivity analyses or inferences on model parameters.
A1 Basin computation
Algorithm 5 finds which basin each node of the grid belongs to by assigning them a label. One unique label is defined (here by an integer) for each basin.

A2 Basin linkage
Algorithm 6 creates the graph of basins by linking together each pair of adjacent basins. It also finds the passes of lowest elevation between those adjacent basins. Note that the links are undirected, such that Links.contains((b0, b1)) == Links.contains((b1, b0)).

The code used for the implementation of the algorithm, examples, and benchmarks presented in this paper is available here: https://github.com/fastscape-lem/flow-routing-depressions (last access: 13 May 2019; Cordonnier et al., 2019). Note that this read-only repository contains a snapshot version of the fastscapelib library that has been extracted for reproducibility purposes. Further maintenance and new developments will happen in the fastscapelib's main repository: https://github.com/fastscape-lem/fastscapelib (last access: 12 March 2019; Bovy and Braun, 2019).
GC designed the algorithm and implemented it including the examples/benchmarks presented in this paper; BB also worked on the implementation. GC and BB worked on the redaction of the paper with contributions by JB, and all authors contributed to fruitful discussions throughout this study, especially JB, who provided many test conditions and use cases.
The authors declare that they have no conflict of interest.
We thank the reviewers for their helpful comments that greatly improved this article.
This paper was edited by Greg Hancock and reviewed by two anonymous referees.
Banninger, D.: Technical Note: Water flow routing on irregular meshes, Hydrol. Earth Syst. Sci., 11, 1243–1247, https://doi.org/10.5194/hess-11-1243-2007, 2007. a
Barnes, R.: Parallel Priority-Flood depression filling for trillion cell digital elevation models on desktops or clusters, Comput. Geosci., 96, 56–68, https://doi.org/10.1016/j.cageo.2016.07.001, 2016. a, b
Barnes, R.: RichDEM: Terrain Analysis Software, available at: http://github.com/r-barnes/richdem (last access: 6 November 2018), 2018. a
Barnes, R., Lehman, C., and Mulla, D.: Priority-flood: An optimal depression-filling and watershed-labeling algorithm for digital elevation models, Comput. Geosci., 62, 117–127, https://doi.org/10.1016/j.cageo.2013.04.024, 2014a. a, b, c, d, e, f, g, h, i, j
Barnes, R., Lehman, C., and Mulla, D.: An efficient assignment of drainage direction over flat surfaces in raster digital elevation models, Comput. Geosci., 62, 128–135, https://doi.org/10.1016/j.cageo.2013.01.009, 2014b. a
Boruvka, O.: O jistém problému minimálním, Pràce Moravské pr̆ìrodovĕdecké spolec̆nosti, 3, 37–58, 1926. a
Bovy, B. and Braun, J.: Fastscapelib, available at: https://github.com/fastscape-lem/fastscapelib, last access: 12 March 2019. a
Braun, J. and Willett, S. D.: A very efficient O (n), implicit and parallel method to solve the stream power equation governing fluvial incision and landscape evolution, Geomorphology, 180, 170–179, https://doi.org/10.1016/j.geomorph.2012.10.008, 2013. a, b, c, d
Campforts, B. and Govers, G.: Keeping the edge: A numerical method that avoids knickpoint smearing when solving the stream power law, J. Geophys. Res.-Earth Surf., 120, 1189–1205, https://doi.org/10.1002/2014JF003376, 2015. a
Cordonnier, G., Braun, J., Cani, M.-P., Benes, B., Galin, E., Peytavie, A., and Guérin, E.: Large scale terrain generation from tectonic uplift and fluvial erosion, Comput. Graph. Forum, 35, 165–175, https://doi.org/10.1111/cgf.12820, 2016. a
Cordonnier, G., Bovy, B., and Braun, J.: A versatile, linear complexity algorithm for flow routing in topographies with depressions (code), available at: https://github.com/fastscape-lem/flow-routing-depressions, last access: 13 May 2019. a
Jenson, S. and Domingue, J.: Extracting topographic structure from digital elevation data for geographic information system analysis, Photogram. Eng. Remote Sens., 54, 1593–1600, 1988. a, b
Jones, N., Wright, S., and Maidment, D.: Watershed delineation with triangle-based terrain models, J. Hydraul. Eng., 116, 1232–1251, https://doi.org/10.1061/(ASCE)0733-9429(1990)116:10(1232), 1990. a
Kruskal, J. B.: On the shortest spanning subtree of a graph and the traveling salesman problem, P. Am. Mathem. Soc., 7, 48–50, 1956. a
Lindsay, J. B.: Efficient hybrid breaching-filling sink removal methods for flow path enforcement in digital elevation models, Hydrol. Process., 30, 846–857, https://doi.org/10.1002/hyp.10648, 2016. a, b, c
Mareš, M.: Two linear time algorithms for MST on minor closed graph classes, ETHZ, Institute for Mathematical Research, 2002. a, b, c, d, e, f
O'Callaghan, J. and Mark, D.: The extraction of drainage networks from digital elevation data, Comput. Vis. Graph. Image Proc., 28, 323–344, https://doi.org/10.1016/S0734-189X(84)80011-0, 1984. a
Quinn, P., Beven, K., Chevallier, P., and Planchon, O.: The prediction of hillslope flowpaths for distributed hydrological modeling using digital terrain models, Hydrol. Process., 5, 59–80, https://doi.org/10.1002/hyp.3360050106, 1991. a
Rieger, W.: A phenomenon-based approach to upslope contributing area and depressions in DEMs, Hydrol. Process., 12, 857–872, https://doi.org/10.1002/(SICI)1099-1085(199805)12:6<857::AID-HYP659>3.0.CO;2-B, 1998. a
Sambridge, M.: Geophysical inversion with a neighbourhood algorithm-I. Searching a parameter space, Geophys. J. Int., 138, 479–494, https://doi.org/10.1046/j.1365-246X.1999.00876.x, 1999. a
Tarboton, D.: A new method for the determination of flow directions and upslope areas in grid digital elevation models, Water Resour. Res., 33, 309–319, https://doi.org/10.1029/96WR03137, 1997. a
Tucker, G. E. and Hancock, G.: Modelling landscape evolution, Earth Surf. Process. Landf., 35, 28–50, https://doi.org/10.1002/esp.1952, 2010. a
Wei, H., Zhou, G., and Fu, S.: Efficient Priority-Flood depression filling in raster digital elevation models, Int. J. Dig. Earth, 0, 1–13, https://doi.org/10.1080/17538947.2018.1429503, 2018. a, b, c, d, e, f, g, h, i
Zhou, G., Sun, Z., and Fu, S.: An efficient variant of the Priority-Flood algorithm for filling depressions in raster digital elevation models, Comput. Geosci., 90, 87–96, https://doi.org/10.1016/j.cageo.2016.02.021, 2016. a, b, c, d, e, f
Zhou, G., Liu, X., Fu, S., and Sun, Z.: Parallel identification and filling of depressions in raster digital elevation models, Int. J. Geogr. Inform. Sci., 31, 1061–1078, https://doi.org/10.1080/13658816.2016.1262954, 2017. a, b





