the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Alluvial channel response to environmental perturbations: fill-terrace formation and sediment-signal disruption
Sara Savi
Andrew D. Wickert
Aaron Bufe
Taylor F. Schildgen
The sensitivity of fluvial systems to tectonic and climatic boundary conditions allows us to use the geomorphic and stratigraphic records as quantitative archives of past climatic and tectonic conditions. Thus, fluvial terraces that form on alluvial fans and floodplains as well as the rate of sediment export to oceanic and continental basins are commonly used to reconstruct paleoenvironments. However, we currently lack a systematic and quantitative understanding of the transient evolution of fluvial systems and their associated sediment storage and release in response to changes in base level, water input, and sediment input. Such knowledge is necessary to quantify past environmental change from terrace records or sedimentary deposits and to disentangle the multiple possible causes for terrace formation and sediment deposition. Here, we use a set of seven physical experiments to explore terrace formation and sediment export from a single, braided channel that is perturbed by changes in upstream water discharge or sediment supply, or through downstream base-level fall. Each perturbation differently affects (1) the geometry of terraces and channels, (2) the timing of terrace cutting, and (3) the transient response of sediment export from the basin. In general, an increase in water discharge leads to near-instantaneous channel incision across the entire fluvial system and consequent local terrace cutting, thus preserving the initial channel slope on terrace surfaces, and it also produces a transient increase in sediment export from the system. In contrast, a decreased upstream sediment-supply rate may result in longer lag times before terrace cutting, leading to terrace slopes that differ from the initial channel slope, and also lagged responses in sediment export. Finally, downstream base-level fall triggers the upstream propagation of a diffuse knickzone, forming terraces with upstream-decreasing ages. The slope of terraces triggered by base-level fall mimics that of the newly adjusted active channel, whereas slopes of terraces triggered by a decrease in upstream sediment discharge or an increase in upstream water discharge are steeper compared to the new equilibrium channel. By combining fill-terrace records with constraints on sediment export, we can distinguish among environmental perturbations that would otherwise remain unresolved when using just one of these records.
- Article
(16814 KB) - Full-text XML
-
Supplement
(210 KB) - BibTeX
- EndNote
Sediment-routing systems are commonly subdivided into three zones: a sediment-production zone, typically a mountainous region; a transfer zone of alluvial and fluvial systems that transport and/or temporarily store sediment; and a sedimentation (or deposition) zone, comprising continental or oceanic basins (Fig. 1; Allen, 2017; Castelltort and Van Den Driessche, 2003). Because climate and tectonics can affect sediment production rates, any changes in those conditions may lead to the formation of fluvial terraces in the transfer zone or changes in sedimentation rates in the deposition zone (Alloway et al., 2007; Bull, 1990; Scherler et al., 2015; Zhang et al., 2001). Many past studies have used such records to reconstruct paleoenvironmental conditions (fluvial terraces: Litty et al., 2016; Poisson and Avouac, 2004; Schaller et al., 2004; sedimentation rates: Hardy et al., 1996; Zhang et al., 2001). Quantitative interpretations of either record, however, require a clear understanding of how terraces are formed or how sedimentary signals are altered in the transfer zone (Romans et al., 2016, and references therein). In addition, both records suffer from ambiguity, because variability in different environmental parameters can produce similar sedimentary responses. For example, changes in either sediment or water inputs can create fill terraces (Scherler et al., 2015) and affect sediment deposition rates (e.g., Armitage et al., 2011; Simpson and Castelltort, 2012).
Alluvial rivers adjust their slope and width with respect to the local base level such that, in a graded (steady) state, the incoming water discharge (Qw) can transport the incoming sediment supply (Qs,in) downstream (Buffington, 2012; Gilbert, 1877; Lane, 1955; Mackin, 1948). When graded, the slope (S) scales nearly linearly with the ratio of Qs,in and Qw (e.g., Blom et al., 2017; Malatesta and Lamb, 2018; Parker, 1979; Wickert and Schildgen, 2019):
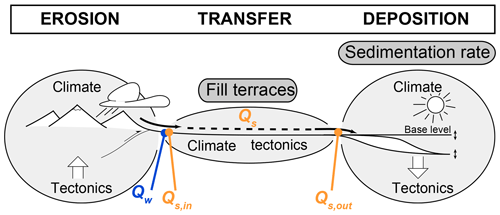
Figure 1Schematic summary of a sediment-routing system and records of landscape evolution. Sediment-routing systems are typically subdivided into three zones: the sediment production (erosion) zone, the sediment transfer zone, and the sediment deposition zone (Allen, 2017; Castelltort and Van Den Driessche, 2003). As sediment production is thought to vary with environmental conditions, changes in those conditions might be preserved in sedimentary records in the transfer zone (e.g., fill terraces) or deposition zone (e.g., sedimentation rates). Complications arise, however, as alluvial rivers within the transfer zone continuously adjust their channel geometry to the incoming water discharge (Qw) and sediment supply (Qs,in) through sediment deposition or remobilization and thus modify the sedimentary signal. The amount of upstream sediment supply combined with additional sediment remobilized within the transfer zone minus the amount of sediment deposited in the transfer zone determines how much sediment is discharged from the transfer zone to the deposition zone (Qs,out). Figure modified from Castelltort and Van Den Driessche (2003).
Changes in boundary conditions (Qw, Qs,in, and base level) therefore cause alluvial rivers to adjust their geometries through sediment deposition (aggradation) or incision, until a new graded profile is reached. Incision or aggradation result from the dependence of bedload-transport capacity on slope and water discharge (Meyer-Peter and Müller, 1948). For example, if Qw increases while Qs,in is held constant, the transport capacity exceeds Qs,in, which leads to the entrainment of additional sediment from the channel bed and thus incision. As incision proceeds, the channel slope decreases until the transport capacity drops to match Qs,in. Conversely, if Qs,in exceeds the transport capacity of the channel, sediment will be deposited to steepen the channel, thus increasing the transport capacity until it matches Qs,in. These adjustments can be recorded through (1) fill-terrace formation in the transfer zone (e.g., Bridgland and Westaway, 2008; Bull, 1990; Merritts et al., 1994) and (2) changes in sediment export to basins (e.g., Allen, 2008; Castelltort and Van Den Driessche, 2003; Romans et al., 2016).
Fluvial–fill terraces form when rivers incise their formerly deposited sediments (Bull, 1990; Howard, 1959), preserving former channel floodplains as terrace surfaces in a process we call “terrace cutting”. Such changes in channel-bed elevation can be triggered by changes at the upstream end of the river, namely the sediment-to-water-discharge ratio, (Eq. 1; e.g., Dey et al., 2016; Scherler et al., 2015; Schildgen et al., 2016; Tofelde et al., 2017), or by base-level changes at the downstream end (e.g., Fisk, 1944; Merritts et al., 1994; Shen et al., 2012). Drivers for terrace formation through the first mechanism include climatically driven variability in Qw (Hanson et al., 2006; Penck and Brückner, 1909; Scherler et al., 2015; Schildgen et al., 2016; Tofelde et al., 2017) and variability in Qs,in, due to, for example, changes in regolith-production rates on hillslopes (Bull, 1991; Norton et al., 2016; Savi et al., 2015), changes in vegetation cover (Fuller et al., 1998; Garcin et al., 2017; Huntington, 1907), exposure of additional regolith following glacier retreat (Malatesta et al., 2018; Malatesta and Avouac, 2018; Savi et al., 2014; Schildgen et al., 2002), or changes in landslide activity (e.g., Bookhagen et al., 2006; McPhillips et al., 2014; Scherler et al., 2016; Schildgen et al., 2016). River incision and terrace cutting through an upstream-migrating knickzone have been related to changes in glacioeustatic sea level (Fisk, 1944; Merritts et al., 1994; Shen et al., 2012) or lake level (Farabaugh and Rigsby, 2005). In some cases, internal dynamics of the system, sometimes referred to as “autogenic processes”, lead to terrace formation that cannot be directly linked to external forcing (e.g., Erkens et al., 2009; Limaye and Lamb, 2016; Malatesta et al., 2017; Patton and Schumm, 1981; Womack and Schumm, 1977).
When studying terraces in the field, it can be difficult to distinguish between terraces that mark a sudden switch from aggradation or stable conditions to incision (“fill-top” terraces of Howard, 1959) and those that preserve surfaces that were cut by a river moving laterally during a period of overall incision (“fill-cut” terraces of Bull, 1990, and Pazzaglia, 2013). In the latter case, there can be a substantial lag between the onset of the environmental perturbation and the abandonment of the terrace surface (e.g., Steffen et al., 2010, 2009). Consequently, from fill terraces alone, both the formation mechanism (change in Qw, Qs,in, or base level) and the timing of the perturbation can be ambiguous.
Numerical and experimental work has demonstrated that the geometrical adjustment of alluvial rivers to external perturbations not only creates fluvial terraces, but also affects sediment discharge at the outlet (Qs,out; Allen and Densmore, 2000; Armitage et al., 2013, 2011; Bonnet and Crave, 2003; Simpson and Castelltort, 2012; Tucker and Slingerland, 1997; van den Berg van Saparoea and Postma, 2008; Wickert and Schildgen, 2019), which may be recorded by changes in sedimentation rates in the deposition zone. For example, increases in either Qw or Qs,in increase Qs,out (Allen and Densmore, 2000; Armitage et al., 2011, 2013; Bonnet and Crave, 2003; Simpson and Castelltort, 2012), but each has a characteristic signature. Whereas a change in Qs,in triggers a permanent change in Qs,out, a change in Qw leads to a transient change in Qs,out (Armitage et al., 2011; Bonnet and Crave, 2003; Wickert and Schildgen, 2019). However, because environmental forcings can be cyclic rather than step changes, it can be difficult to relate variability in sedimentation rates to a distinct forcing. Moreover, changes in Qs,out in response to changes in Qs,in or Qw may be buffered, amplified, or directly transmitted through sediment-routing systems (Armitage et al., 2013; Godard et al., 2013; Romans et al., 2016, and references therein; Simpson and Castelltort, 2012). We propose that, to correctly interpret changes in sedimentation rates, the modifications of Qs,in within the transfer zone (then referred to as Qs) due to sediment deposition (channel aggradation) and remobilization (channel incision) must be understood.
The long temporal and broad spatial scales of fill-terrace formation and sediment deposition preclude direct observations of their potential links in nature. Numerical models provide an inroad to understand the evolution of river long profiles and/or Qs,out after perturbations (Blom et al., 2017, 2016; Malatesta et al., 2017; Simpson and Castelltort, 2012; Slingerland and Snow, 1988; Wickert and Schildgen, 2019), but most simulate river-profile evolution without taking into account modifications of channel width or terrace formation (Blom et al., 2017, 2016; Simpson and Castelltort, 2012; Slingerland and Snow, 1988; Wickert and Schildgen, 2019). In addition, most numerical models for river-profile evolution rely on equations derived for the steady-state case. As such, they may not accurately simulate transient responses, which are important for capturing terrace formation and modifications of Qs,in in the transfer zone. Physical experiments provide an alternative approach to studying the dynamics of the transfer zone, including terrace formation (Baynes et al., 2018; Frankel et al., 2007; Gardner, 1983; Lewis, 1944; Mizutani, 1998; Schumm and Parker, 1973; Wohl and Ikeda, 1997) and the evolution of Qs,out (Bonnet and Crave, 2003; van den Berg van Saparoea and Postma 2008). Most experimental studies have tested the cutting of terraces due to base-level fall (BLF; Frankel et al., 2007; Gardner, 1983; Schumm and Parker, 1973) or explained their cutting through autogenic processes (Lewis, 1944; Mizutani, 1998). Only one experimental study by Baynes et al. (2018) investigated terrace formation as a response to changes in Qs,in or Qw, but this study focused on vertical incision into bedrock and strath-terrace cutting. Van den Berg van Saparoea and Postma (2008) and Bonnet and Crave (2003) investigated the effects of variability in Qw and Qs,in on the topographic evolution and Qs,out, but neither considered how these processes may be linked to terrace formation. To our knowledge, there are no experimental studies that consider the combined evolution of two records of landscape evolution – fill terraces in the transfer zone and sediment discharge to the deposition zone – in response to environmental perturbations.
In this study, we present results from seven physical experiments of the transfer zone, represented by a single braided channel in noncohesive sediment, in which we perturb Qw, Qs,in, and base level. We investigate the timing and geometrical response (slope, width) of the alluvial channel in the transfer zone (with a particular focus on fill-terrace cutting) and patterns and response rates of Qs,out, with a particular focus on how the records may be linked and if a combination of both records can be diagnostic of specific changes in boundary conditions.
To test the impact of different external forcings on fill-terrace formation in the transfer zone and sediment export to the deposition zone, we performed seven experiments at the Saint Anthony Falls Laboratory in Minneapolis, USA, in 2015 (Table 1). The experimental setup consisted of a wooden box with dimensions of 4 m × 2.5 m × 0.4 m (Fig. 2a) that was filled with quartz sand with a mean grain size of 144 µm. At the inlet, we supplied sand and water through a cylindrical wire-mesh diffuser filled with gravel to ensure sufficient mixing of sand and water. Water discharge (Qw) and sediment supply (Qs,in) could be regulated independently of one another. At the downstream end, water and sand (Qs,out) exited through a 20 cm wide gap that opened onto the basin floor below. This downstream sink was required to avoid deltaic sediment deposition that would, if allowed to grow, eventually raise the base level of the upstream fluvial system. At the beginning of each experiment, we shaped an initial channel by hand (Fig. 2a) and ran the experiment under reference conditions ( mL s−1, mL s−1) for 240 min. This runtime was sufficient to reach a quasi-steady state in which the average Qs,out approximately equaled Qs,in. After this spin-up phase, the channel had a uniform equilibrium slope of approximately 7 %.
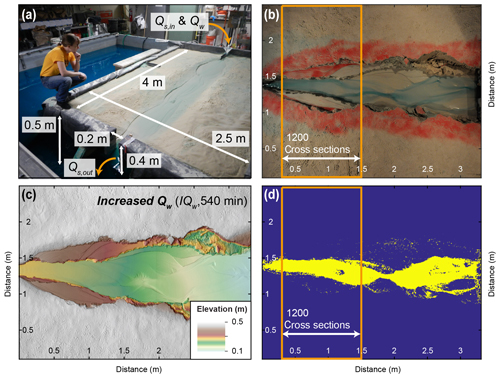
Figure 2Experimental setup, data collection, and analyses. (a) Overview of experimental setup. Sediment supply (Qs,in) and water discharge (Qw) can be regulated separately. For all but the base-level fall (BLF) experiment, the base level was fixed. Water and sediment fell off of an edge at the outlet. For the BLF experiment (shown in the picture), the base level was controlled through the water level in the surrounding basin. (b) Overhead photograph of the IQw experiment taken directly before the scan shown in panel (c). (c) Digital elevation model (DEM) derived from laser scans showing the final topography of the increased water (IQw) experiment. The surface was covered with a thin layer of red sand before the instant increase in Qw was performed. The remnants of red sand on the terraces indicate no further reworking after the onset of increased discharge. (d) Overhead photographs were turned into binary (wet, dry) images from which the average channel width within the indicated area (orange frame) was calculated.
Every 30 min, we stopped the experiments to measure topography using a laser scanner mounted on the railing of the basin that surrounded the wooden box. Digital elevation models (DEMs) created from the scans have a horizontal and vertical resolution of 1 mm (Fig. 2c). Using those DEMs, we measured the evolution of channel cross-sectional profiles, longitudinal channel profiles, and surface slopes. Long profiles were calculated by extracting the lowest elevation point in each cross section at 1 mm increments. By plotting elevation against the distance down the long axis of the box rather than against channel length, resulting slopes are slightly overestimated due to the minor sinuosity of the channels. To directly compare terrace and channel slopes, we extracted 5 cm wide swath profiles along the terrace surfaces and the equivalent stretch of the modern channel. Where terraces were narrower than 5 cm, we reduced this swath width. Slopes were calculated based on a linear fit through the mean elevation profiles. To assess uncertainties, the root mean square error (RMSE) was calculated between the linear model and the observed data.
Overhead photos were taken every 20 s with a fish-eye lens (Fig. 2b). Distortions of the photos were orthorectified in Adobe Photoshop, and photos were resampled at 1 mm horizontal resolution to directly overlap with the laser scans. Photos were turned into binary images with values of 1 for wet pixels and 0 for dry pixels. This binarization was performed by transforming the RGB (red, green, blue) images into HSV (hue, saturation, value) images and then manually defining a hue cutoff for each experiment that best separates wet and dry pixels in the image (Fig. 2d). To distinguish wet and dry pixels by color, the supplied water was dyed blue (Fig. 2b). From the binary images, the number of wet pixels in each cross section (perpendicular to the basin margin and therefore to the average flow direction) were counted. Analyses were restricted to the areas within the orange box (Fig. 2b, d), because terraces mainly developed in this part of the channel and because we considered this sector at the upstream side of the basin to be least affected by the fixed location of the outlet. To calculate average channel width, the average number of wet pixels in 1200 cross sections were counted and are reported with 1 standard deviation. No overhead photos were taken for the Ctrl_1 experiment because of an error in the camera installation.
We manually measured Qs,out at 10 min intervals by collecting the discharged sediment in a container over a 10 s period and measuring its volume. This approach allowed us to estimate whether the system had returned to steady state () during the runs. At the same 10 min interval, we measured bed elevation at the inlet and at the outlet to estimate the spatially averaged channel slope. We interpreted a constant slope for over more than 30 min as additional evidence for a graded (steady state) channel. Manual slope and Qs,out measurements can be found in the Supplement. Topographic scans, overhead photos, and time-lapse movies of the experimental runs as well as experiment documentation are available through the SEAD Internal Repository (Tofelde et al., 2019).
We ran seven experiments to monitor how changes in Qs,in, Qw, and base level affect channel adjustment, the evolution of fill terraces along the main stem, and sediment discharge at the outlet (Qs,out) through time. The experiments are summarized in Table 1. To investigate the effect of Qw, we ran two separate experiments: in one experiment we doubled Qw (IQw= increase discharge) to 190 mL s−1 at 240 min (end of the spin-up time) and in the other experiment we first halved Qw to 48 mL s−1 at 240 min and then returned to the initial 95 mL s−1 at 480 min (DQw_IQw= decrease discharge, increase discharge). To test the effect of Qs,in, we ran one experiment in which we reduced Qs,in by 83 % to 0.22 mL s−1 ( decrease sediment supply) at 240 min and another one in which we first doubled Qs,in to 2.6 mL s−1 at 240 min and then halved Qs,in again to the initial 1.3 mL s−1 at 480 min ( increase sediment supply, decrease sediment supply). All Qs,in and Qw changes were imposed instantaneously, resulting in a step function in the forcing (Table 1). Immediately before imposing these changes, we covered the near-channel surface with a thin layer of red sand to optically identify the area that was reworked after the change. This method allowed us to distinguish visually between fill-top (covered in red sand) and fill-cut terraces (red sand removed due to continuous overwash). We ran one experiment in which we dropped the base level by 10 cm gradually over 20 min starting at 240 min, resulting in a base-level lowering rate of 0.5 cm min−1 (BLF). For this experiment, we started with a base level higher than in the initial setting by flooding the basin surrounding the wooden box (Fig. 2a). The final base level equaled that of the other experiments. In this experiment, the red sand was applied immediately before the onset of base-level lowering. Additionally, we performed two control experiments in which we made no changes to the initial conditions to investigate whether terraces would form in our experiment without any change in external forcing (Ctrl_1, Ctrl_2).
Fluvial terraces were cut in the experimental runs IQw, DQw_IQw (in the IQw phase), DQs,in, (in the DQs,in phase), and BLF (Figs. 3, 4). No terraces were formed after the spin-up time of Ctrl_1 and Ctrl_2. The terraces visible in the cross section of Ctrl_2 formed in response to incision during the spin-up phase and did not substantially develop after 240 min (Fig. 4b, red line). We named the terraces to the left of the channel (in downstream direction) TL and the terraces to the right TR. In all terrace-forming experiments, both fill-top (red sand) and fill-cut terraces (red sand removed) formed (Fig. 3). Only in the IQw, DQw_IQw, and experiments were the fill-top terraces preserved as the most extensive terrace surface, at least on one side of the channel (Fig. 3a, b, d). In the DQs,in experiment, only a fraction of the fill-top terrace (TL) survived the transient channel-adjustment phase (Fig. 3c). In all experiments that experienced upstream perturbation, fill-top and fill-cut terraces formed only in the upstream half of the sandbox. In contrast, in the BLF experiment, terraces formed in the downstream channel reach immediately after the onset of base-level drop but were mostly destroyed within 30 min (Fig. 3e, g). Later during the BLF experiment, terraces formed in the upstream portion of the sandbox (Fig. 3f).
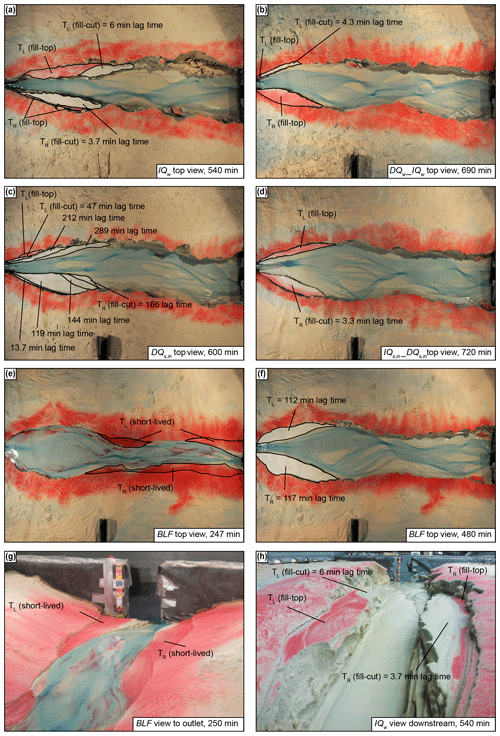
Figure 3Fill terraces formed during experimental runs. (a–d) Top view of terraces that formed due to upstream perturbations. Remnants of red sand on the terrace surfaces indicate areas that have not been flooded after the change in boundary condition was performed (i.e., fill-top terrace). The other terrace surfaces were cut with the indicated lag times (fill-cut terraces). (e–f) During the base-level fall (BLF) experiment, terraces at the downstream end were abandoned instantly after the onset of base-level fall (250 min = 10 min after onset of BLF). Those terraces were destroyed shortly after they were cut. A new set of terraces formed in the upstream part ca. 112 and 117 min after the onset of BLF. (g–h) Downstream view for the BLF (g) and IQw (h) experiments.
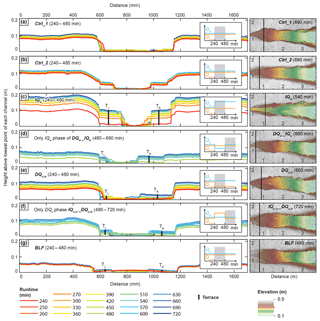
Figure 4Evolution of cross sections in the upper part of the channel (left panel). In each cross section, the lowest point is set equal to zero to track incision. The color scheme represents absolute experimental runtime, beginning after the spin-up phase (i.e., 240 min). For better comparison, we plot a maximum of 240 min for all experiments, despite longer recordings for some of the runs. Exact locations of cross sections are indicated by the black lines in the DEMs displaying the last scan of each experiment (right panel). Cross sections have been chosen at the terrace midpoints and thus vary slightly between the experiments. The times given in parentheses are the absolute experiment runtimes.
Fill-cut terrace cutting lagged minutes to hours behind the onset of the imposed perturbation (Fig. 3). We determined lag times from overhead photos, defined as the time interval between the onset of the perturbation (at minute 240 or 480) and the final time that the future terrace surface was occupied by water. In the two experiments during which we changed Qw and in the experiment, the cutting of fill-cut terraces began within 6 min after the change in boundary conditions (Fig. 3a, b, d). In the IQw experiment, for example, the majority of the TL terrace is a fill-top terrace (0 min lag time) and only a small part at the downstream end was occupied until 6 min after perturbation (Fig. 3a, h). In the DQs,in experiment, however, several fill-cut terraces formed successively with lag times between ∼14 and 289 min (Fig. 3c). This experiment was the only one in which a sequence of terraces, instead of a single major surface, developed. In the BLF experiment, terrace cutting in the upstream part of the basin began 112 and 117 min after the onset of base-level lowering (Fig. 3f).
Fill-terrace formation requires changes in the channel-bed elevation and width of the active floodplain. In our experiments, sediment deposition (aggradation) or erosion (incision) altered the channel-bed elevation (Fig. 5). However, these changes were not uniform along the channel. In the runs Ctrl_1 and Ctrl_2, the longitudinal profiles were stable over time and experienced only minor lowering in bed elevation (max. 4 cm) at their upstream ends (Fig. 5a, b). A sudden increase in Qw (IQw, and the IQw phase of DQw_IQw) or a decrease in Qs,in (DQs,in, and the DQs,in phase of ) both led to channel incision (Fig. 5c, d, g, h). This incision was most pronounced at the upstream end, near the changing boundary condition, but not recognizable at the downstream end (Fig. 5d, g, h), where the channel-bed elevation was fixed due to the steady base level. Sediment deposition in the channels followed a decrease in Qw (DQw phase of DQw_IQw) or an increase in Qs,in (IQs,in phase of ), which was, again, most recognizable at the upstream end of the channel (Fig. 5e, f). The drop in base level, however, caused maximum incision at the downstream end, and the incision wave migrated upstream as a diffuse knickzone (Fig. 5i).
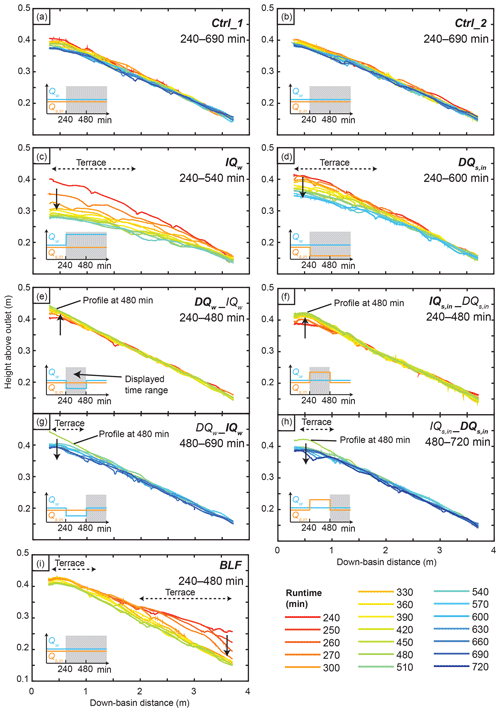
Figure 5Evolution of longitudinal river profiles from minute 240 (end of spin-up phase) onwards. River profiles were extracted from the laser scans. Laser scans were recorded every 30 min, and an additional two scans at 10 and 20 min after the initiation of the base-level fall were conducted during the BLF experiment. Dashed arrows indicate the down-basin distance along which terraces formed. Solid arrows indicate modes of aggradation or incision. Note that the DQw_IQw and were split into two panels each, with one panel representing each phase.
Channel slope and width changes were observed in the absence of external perturbations. Channel slopes in the Ctrl_1 and Ctrl_2 marginally decreased after the 240 min spin-up time from ∼0.074 and 0.071, respectively, to around 0.070 and 0.067 (∼6 % reduction; Fig. 6a). As such, we consider any change in slope after the spin-up time that is on the same order as those observed in Ctrl_1 and Ctrl_2 as ongoing adjustment to the reference condition as opposed to the result of an external perturbation. Channel width in the control experiments varied slowly between ca. 20 and 35 cm.
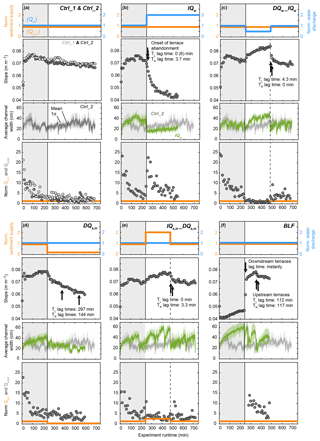
Figure 6Input parameters and evolution of channel slope, channel width, and Qs,out during the experiments. Input sediment (Qs,in, orange solid line) and water discharge (Qw, blue solid line) were normalized to the reference input values ( mL s−1 and mL s−1). Slope (S, grey circles) was calculated based on the bed-elevation difference between the inlet and the outlet divided by the length of the system. Channel elevation measurements for slope calculations were performed manually during the runs. Black arrows indicate times when terraces in the upstream part of the sandbox started to be cut. Channel width was calculated as the mean number (solid lines) of wet pixels in each of 1200 cross section within the box indicated in Fig. 2b and d. The colored shaded areas around the curves indicate the standard deviation of the 1200 measurements. The evolution of width without any external perturbation (Ctrl_2) is plotted for comparison with each other experiment in which external conditions were changed (b–f). Note that no measurements are available for the Ctrl_1 experiment due to issues with the installation of the overhead camera. Sediment discharge at the outlet (Qs,out, grey circles) during the experimental runs is compared to input sediment (Qs,in, orange solid line); both were normalized to reference input values ( mL s−1). Note that no Qs,out measurements are available for the first 280 min of the BLF experiment, as no sample collection was possible during the flooding of the surrounding basin during base-level regulations (Fig. 2a).The first 240 min of each experiment was adjustment to the reference settings (grey box) and was not included in the analyses.
External perturbations in water and sediment inputs forced the channel width and slope to evolve. An instant doubling of Qw (IQw; Fig. 6b) resulted in a rapid decrease in channel slope that decayed exponentially as the channel approached a new graded state. After approximately 480 min, the slope was reduced from ∼0.072 to ∼0.043 (40 % reduction), and new stable conditions were reached. The doubling of Qw also triggered an instant narrowing of the channel from ∼35 to ∼15 cm (∼57 % decrease), followed by subsequent slow widening.
In contrast, suddenly reducing Qw to half its initial value (DQw_IQw; Fig. 6c) increased the channel slope from ∼0.072 to ∼0.085 (18 % increase) between 240 and 480 min runtime and caused the channel to widen from about 25 to about 45 cm (∼80 % increase) during the same time period. The subsequent doubling in Qw back to its initial value triggered a rapid reduction in slope back to the initial ∼0.072 (∼15 % reduction, again following an exponential decay) and an instantaneous narrowing of the channel (∼45 % reduction) followed by slow widening.
Reducing Qs,in by 83 % (DQs,in; Fig. 6d) triggered a decrease in the channel slope at a slower rate than in the IQw run; and the new slope stabilized around 0.060 (24 % reduction from the initial 0.079). An instantaneous decrease in channel width also occurred, but this change was again less pronounced than what we observed in the IQw experiment (∼33 % reduction). We detected no subsequent widening of the channel.
Finally, increasing Qs,in (; Fig. 6e) led to channel steepening from a slope of 0.070 to about 0.078 (11 % increase) and increased channel width from about 30 to about 55 cm (∼83 % increase). The subsequent reduction in Qs,in decreased the channel slope and caused an instantaneous channel narrowing to <30 cm, followed by subsequent widening back to the initial width of ∼30 cm.
During the base-level fall experiment (BLF; Fig. 6f), mean channel slope instantly and rapidly increased after the onset of base-level fall from about 0.047 to 0.073 (55 % increase) and continued to increase at a slower rate to about 0.08, before decreasing back to 0.072. These mean values, however, average over any spatial variability in incision, meaning that they do not resolve the details of the diffusive propagation of the knickzone. Beyond impacts on slope, the drop in base level resulted in a sudden decrease in channel width, followed by three cycles of channel widening and narrowing. In summary, we observed that an increase in Qw and a decrease in Qs,in resulted in an immediate decrease in channel slope (through upstream incision) and an instant reduction in channel width, whereas a drop in base level caused an increase in channel slope (through downstream incision) and a reduction in channel width (Fig. 6).
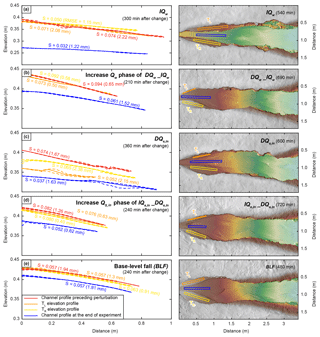
Figure 7Elevation profile and slope comparison of terrace surfaces and active channels. Elevation profiles are given as mean (solid lines) and minimum and maximum values (dashed lines), extracted along 5 cm wide swaths as indicated on the right panel. Swath width was reduced in two cases of too narrow terraces to 1 cm (DQw_IQw TL terrace) and 2 cm (DQs,in TL terrace). TL and TR indicate terraces on one side each and refer to labels of lag times given in Figs. 3 and 6. Slopes were calculated based on a linear fit through the mean elevation profiles. Numbers in parentheses give the RMSE between the linear fit and the measured data. For the four experiments in which upstream conditions changed (a–d), the slopes of the terraces are steeper than those of the active channel at the end of the experiment. In contrast, in the BLF experiment, slopes of the terraces and the active channel are about the same. Note the different y axis for the IQw run that was necessary to display the deep incision. Colors for elevations in the right panel are the same as those in Fig. 4.
To analyze how well terrace surfaces represent channel slopes immediately preceding the time of perturbation, we compared the elevation profiles of the terraces on each side of the channel (yellow and orange lines) with the channel that existed at the onset of the perturbation (red line) (Fig. 7). We sampled elevations across the most extensively preserved terrace surface, regardless of its lag time, in a way that is similar to terrace mapping in the field. In experiments with increasing Qw (IQw, IQw phase of DQw_IQw) or base-level changes (BLF), the elevation profiles of the terraces are similar to the initial floodplain profile (Fig. 7a, b, and e). In cases of changes in Qs,in (DQs,in, DQs,in phase of ), the terraces were cut at lower elevations than the former channel (Fig. 7c, d). In the DQs,in experiment, fill-cut terraces on either side of the channel formed at different elevations, with one surface about 3 cm below the other (Figs. 7c, 4e). In contrast, terrace surfaces in the other four experiments are at approximately the same elevation (Figs. 4, 7). Despite similar elevations, the slope differences between TL and TR range from about 5 % () to 33 % (IQw). When comparing terrace slopes to the active channel slopes at the end of each run (blue lines), terrace slopes are steeper (by 20 %–122 %) in all experiments in which upstream conditions (Qw, Qs,in) changed (Fig. 7a–d). In contrast, the slopes of the terraces and the active channel in the BLF experiment are similar to one another (within 11 %) (Fig. 7e).
Changes in boundary conditions also affected Qs,out (Fig. 6, lowest panels). An instantaneous doubling of Qw (IQw; Fig. 6b) resulted in an instant increase in Qs,out to more than 20 times Qs,in. This rapid increase was followed by an exponential decay down to the initial Qs,out value. A sudden reduction in Qw to half its initial value (DQw_IQw; Fig. 6c) resulted in a decrease in Qs,out. The subsequent doubling in Qw back to its initial value triggered a rapid increase in Qs,out that decayed over time. In contrast, neither the instantaneous reduction in Qs,in by 83 % (DQs,in; Fig. 6d) nor the doubling in Qs,in (; Fig. 6e) triggered a measurable change in Qs,out. For the base-level fall experiment (BLF; Fig. 6f), Qs,out could not be measured before and during the base-level drop because the basin surrounding the wooden box was flooded for this experiment. Qs,out was only measured from minute 280 onwards, which corresponds to minute 40 after the spin-up of the base-level fall. At that time, Qs,out was still about 10 times higher than Qs,in, and Qs,out decreased approximately linearly from that time onwards.
When attempting to use geomorphic or depositional records to reconstruct paleoenvironmental conditions, we face a range of challenges. One challenge is to understand how the information on environmental boundary conditions is translated into the sedimentary record, considering the potential modification of sediment signals during fluvial transport. A second, related challenge is that depositional records and fluvial terraces often cannot unambiguously be associated with a particular forcing mechanism. In the following, we will discuss these two challenges, and we will focus on both records that we monitored in our experiments – fill terraces in the transfer zone and sediment discharge to the deposition zone (Qs,out). Further, we will discuss the use of an integrated set of observations to address these challenges, the limitations that arise when comparing the experimental work to natural settings, and potential implications of our observations for future field studies.
4.1 Terrace formation in the transfer zone
4.1.1 Conditions of terrace formation, lag times, and the preservation of preperturbation channel profiles
The cutting of fluvial–fill terraces requires vertical incision and a simultaneous reduction of the active floodplain width. Whether this occurs depends on the response of alluvial channels to changing boundary conditions, which can include adjustments of slope, wetted perimeter (width and depth), and/or bed-surface texture (grain-size distribution) (e.g., Blom et al., 2017; Buffington, 2012, and references therein; Wickert and Schildgen, 2019). Because the grain-size distribution in our experiments remained constant, we focus our discussion on the externally forced adjustments of channel slope (S) and width (w) during terrace formation.
In our experiments, river incision (with terrace cutting) was driven by an increase in Qw, a decrease in Qs,in, or a fall in base level (Figs. 3–6). In the case of base-level fall, incision began at the downstream boundary and diffused upstream, producing a transient steepening. Enhanced Qw or reduced Qs,in, on the other hand, decreased the channel slope. The evolution of longitudinal channel profiles in our experiments is in agreement with earlier flume studies that investigated channel response to upstream (van den Berg van Saparoea and Postma, 2008) and downstream (Begin et al., 1981; Frankel et al., 2007) perturbations, as well as with numerical models that predict the evolution of longitudinal profiles following variations in Qs,in, Qw, or base level (Blom et al., 2017; Simpson and Castelltort, 2012; Wickert and Schildgen, 2019). In all experiments, incision and terrace cutting coincided with an instantaneous decrease in channel width, while aggradation corresponded to an increase in channel width (Fig. 7).
A common application of fluvial-terrace mapping is to reconstruct paleolongitudinal channel profiles from terrace remnants (e.g., Faulkner et al., 2016; Hanson et al., 2006; Pederson et al., 2006; Poisson and Avouac, 2004). These profiles are thought to be representative of the former channel profiles, ideally reflecting their geometries immediately prior to a perturbation. However, morphological adjustments of a channel to external perturbations require time, such that the geomorphological response can lag behind the changes in environmental parameters (e.g., Blum and Tornqvist, 2000; Tebbens et al., 2000; Vandenberghe, 2003, 1995). The lag time between an external perturbation and the onset of terrace cutting determines how much time the fluvial system has to modify the terrace sediments before their abandonment. In the following, we first discuss the relationship between lag times and the preserved terrace profiles related to upstream perturbations (), followed by those related to downstream perturbations (BLF).
In our experiments, the upstream-perturbation-related terrace surfaces (fill-top and fill-cut terraces) following an increase in Qw had short lag times (≤6 min; Figs. 3a, b and 6b, c) and preserved the channel elevation profiles prior to perturbation well (Fig. 7a, b). Similarly, terrace cutting in the experiment was characterized by short (TR) or no (TL) lag times (Figs. 3d and 6e). The small discrepancy between terrace slopes and initial channel slopes in this experiment (Fig. 7d) is a result of slope variations between the center of the channel belt (where initial and final channel profiles were measured) and the sides of the channel belt, where the terrace slopes were measured. In contrast, terrace cutting in the DQs,in experiment occurred with a delay of several hours, and the terraces were also cut successively (Figs. 3c, 6d). The difference in lag times between the TL and TR terrace of about two and a half hours resulted in different terrace elevations on both sides of the channel, with elevation profiles several centimeters below the channel profile prior to perturbation (Fig. 7c). These results illustrate how short lag times are critical to enable accurate reconstructions of the preperturbation channel profile, which can potentially be used to reconstruct paleoenvironmental conditions. But what determines the duration of the lag time?
The length of the lag time between the perturbation and the abandonment of a terrace surface is expected to depend on the ratio of vertical incision versus lateral erosion. Bufe et al. (2018) and Malatesta et al. (2017) demonstrated that the rate of lateral channel migration scales inversely with the height of valley walls (elevation difference between a terrace surface and the active channel). As such, higher incision rates after a perturbation lead to faster wall-height growth and greater reductions in lateral mobility. Accordingly, fast incision should result in short lag times between the onset of the perturbation and terrace cutting, guaranteeing good preservation of the channel profile that existed prior to the perturbation. In contrast, slow river incision and enhanced lateral channel movement can lead to long lag times, with terrace profiles that reflect a channel profile at some (unknown) phase of adjustment. The incision rate, on the other hand, is thought to be a function of the excess sediment-transport capacity, and sediment-transport capacity should be directly proportional to Qw (Wickert and Schildgen, 2019). Doubling Qw should correspondingly double the sediment-transport capacity and therefore add excess transport capacity equal to the initial capacity. In contrast, halving Qs,in will keep the total transport capacity the same but will reduce the amount of sediment that must be moved by 50 %, thus partitioning 50 % of the initial capacity as excess. Therefore, increases in Qw should, in theory, cause more rapid incision, shorter lag times, and a higher preservation potential for the preperturbation channel profile than a proportionately equal reduction in Qs,in. However, while one of the two experiments with a reduction in Qs,in (DQs,in) is consistent with this theory (Fig. 6d), in the other one (), we observed relatively short lag times (Fig. 6e). These unexpectedly short lag times might be related to how the incision phase was preceded by an aggradation phase (due to an increase in Qs,in). Possibly, the system rapidly settled back to the initial conditions because it had not completely adjusted to the preceding increase in Qs,in.
The lag time between the onset of base-level fall and the cutting of terraces in the upstream reach of the channel is about 115 min (Figs. 3f and 6f), which was the time required for the knickzone to propagate upstream. As such, for terraces related to base-level fall, the temporal lag between the onset of the perturbation and terrace cutting increases with upstream distance. Hence, terrace surfaces created through upstream knickpoint migration are diachronous – become progressively younger upstream despite being a physically continuous unit. Similar results have been reported from field studies (Faulkner et al., 2016; Pazzaglia, 2013). In comparison, incision initiated near-synchronously along the entire experimental channel when triggered by a change in upstream boundary conditions (IQw, DQs,in; Fig. 5c, d). In summary, lag times between the onset of a perturbation and terrace cutting depend on the combination of local incision rates after the perturbation and the trigger for incision (base-level fall vs. a change in upstream conditions).
4.1.2 Terrace geometry as an indicator of perturbation type
Because fluvial–fill terraces result from changes in Qw, changes in Qs,in, or a drop in base level, their presence alone does not indicate which of the parameters changed over time. However, our experimental results revealed differences in terrace geometry between changes in upstream (Qw, Qs,in) versus downstream (BLF) conditions. For terraces related to changes in Qs,in or Qw, the slopes of terrace surfaces are always steeper than the active channel (the new steady state channel after the perturbation), whereas the slope of terraces formed due to downstream perturbations is very similar to that of the active channel (Fig. 7). These observations concur with predictions from theoretical work that suggests a positive scaling of slope and Qs,in and a negative scaling of slope and Qw, while a drop in base level should, after the signal has propagated upstream, result in a slope similar to the channel before the perturbation because of a constant ratio (Lane, 1955; Mackin, 1948; Malatesta and Lamb, 2018; Meyer-Peter and Müller, 1948; Wickert and Schildgen, 2019; Wobus et al., 2010). Similar observations have been made in the field. In the Tien Shan, Poisson and Avouac (2004) found a successive reduction in slope within a terrace sequence, which they related to changes in Qw. In the Central Andes, Pepin et al. (2013) explained downstream-converging terraces (and thus a reduction in terrace-surface slopes) on a piedmont through variability in climatic drivers. In contrast, along the Chippewa River in the USA (a tributary to the Mississippi River), where terrace cutting is linked to base-level fall, Faulkner et al. (2016) found no substantial slope change between the longitudinal profile reconstructed from the terraces and the modern channel.
Our findings support earlier observations that slope comparisons between the terrace surfaces and the active channel could indicate whether an upstream- or a downstream-sourced perturbation caused the cutting of the terraces (Faulkner et al., 2016; Pepin et al., 2013; Poisson and Avouac, 2004; Wobus et al., 2010). However, such comparisons are only informative if the active channel is still graded to the boundary conditions that initiated incision and terrace cutting. In addition, this approach to identifying the terrace-formation mechanism requires negligible or quantifiable tectonic tilting of the terraces after cutting.
4.2 Sediment discharge to the deposition zone
4.2.1 Qs-signal modification in the transfer zone
In steady state, the transfer zone experiences no net sediment deposition or removal of sediment. Hence, when averaged over a certain time, Qs,in equals Qs,out and the signal can be considered to be faithfully transmitted to the deposition zone (e.g., Romans et al., 2016). During geometrical channel adjustments, however, when sediment is either deposited or eroded to adjust the channel slope, Qs,out differs from Qs,in (Fig. 6). This is schematically shown in Fig. 8 by the divergence between the solid line (Qs,in) and circles (Qs,out). Thus, Qs signals can be considered to be modified as long as the transfer zone is in a transient state. The total time of Qs-signal modification depends on two variables: (1) the time a certain transfer zone requires to reach graded conditions again, i.e., the channel response or equilibrium time (Castelltort and Van Den Driessche, 2003; Howard, 1982; Métivier and Gaudemer, 1999; Paola et al., 1992); and (2) the frequency at which boundary conditions (Qw, Qs,in, base level) change. Consequently, if the period of the forcing is shorter than the required response time of the channel reach, the Qs signal will never be faithfully transmitted (Paola et al., 1992).
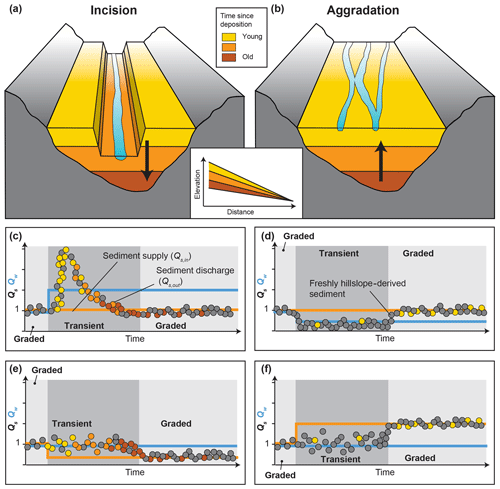
Figure 8Schematic model of the evolution of Qs,out including inferred ages of the sediment. (a, b) Channel geometry and approximate distribution of sediment deposition ages during phases of incision and aggradation. (c–f) Evolution of Qs,out (circles) compared to Qs,in (orange solid line) and Qw (blue solid line) during the transient response phase after perturbation (dark grey), as well as after channel adjustment (light grey). The colors of the circles indicate the age (i.e., storage times before export) of the discharged sediment according to the panels (a) and (b).
4.2.2 Observable changes in sediment export to the deposition zone (Qs,out)
Regardless of whether the Qs signal is faithfully transmitted or modified, we observed changes in Qs,out in our experiments, which would likely be reflected by changes in sedimentation rates within the deposition zone. Enhanced Qs,out, for example, was generated both by an increase in Qw (Fig. 6b) and by a drop in base level (Fig. 6f). Hence, from the Qs,out record alone, the driving mechanism cannot be identified. The temporary Qs,out peak in the IQw experiment (Fig. 6b and schematically in Fig. 8c) resembles the observations of earlier numerical (Armitage et al., 2011, 2013; Tucker and Slingerland, 1997) and experimental work (van den Berg van Saparoea and Postma, 2008; Bonnet and Crave, 2003). In both this earlier work and ours, the peak in Qs,out was generated during the transient phase of slope adjustment. According to Eq. (1), an increase in Qw will decrease channel slope and, therefore, trigger river incision. Because Qs,in was held constant during the experiment, the additional sediment that reached the outlet was remobilized from within the channel, in particular from the upstream part (Fig. 5c, g; Castelltort and Van Den Driessche, 2003; van den Berg van Saparoea and Postma, 2008; Wickert and Schildgen, 2019). In contrast, a decrease in Qw requires a steeper channel slope, which is achieved through sediment deposition within the channel (Fig. 5e). In our experiments, this adjustment appears as a reduction in Qs,out relative to the upstream sediment supply during the transient slope-adjustment phase (Figs. 6c and 8d).
A decrease in Qs,in should, following the achievement of a graded channel profile, reduce Qs,out, whereas an increase in Qs,in should increase Qs,out (Allen and Densmore, 2000; Armitage et al., 2011; Bonnet and Crave, 2003). According to Eq. (1), reducing Qs,in will trigger temporary incision because a lower slope is required to transport less sediment with the same Qw. Conversely, increasing Qs,in without changing Qw will require a steeper transport slope and thus trigger aggradation. Channel incision and slope reduction occurred in the DQs,in experiments (Figs. 5d, h and 6d, e), whereas aggradation and slope increase followed an increase in Qs,in (Figs. 5f and 6e). However, in none of the experiments with variable Qs,in was a clear change in Qs,out recognizable during the transient phase of slope adjustment (Figs. 6d, e and 8e, f). We consider the negative feedback between Qs,in and the bed-elevation change during the transient channel-adjustment phase as the main reason for this lack of response (van den Berg van Saparoea and Postma, 2008; Simpson and Castelltort, 2012). The additional sediment supplied upstream is deposited within the channel, resulting in aggradation, and is therefore not detectable at the outlet. When less sediment is supplied upstream, the channel incises and complements the supplied upstream sediment with remobilized sediment from within the channel, such that once again, no change in Qs,out is detectable at the outlet during the adjustment phase. We did not run the experiments long enough to analyze the adjusted steady-state phase, but we would expect that once the channel has adjusted to new equilibrium conditions, Qs,out will eventually equal Qs,in (Fig. 8e, f; Allen and Densmore, 2000; Armitage et al., 2011; Bonnet and Crave, 2003; Wickert and Schildgen, 2019).
Internal channel dynamics can lead to variability in Qs,out even without external forcing. In the Ctrl_1 and Ctrl_2 experiments, scatter in the Qs,out signal was up to 5 times the value of Qs,in (Fig. 6a). This variability is due to continuous lateral movement of the channel and subsequent bank collapse, which results in stochastic contributions of additional sediment. Lateral channel mobility of a stream varies with water and sediment discharge (Bufe et al., 2018; Wickert et al., 2013). However, if the volume of sediment mobilized from valley walls due to lateral migration is much larger than the change in Qs,in, then no clear signal in Qs,out might be recognizable, even after channel adjustment. The channel instead will continually adjust to the stochastic lateral input of sediment.
Regarding Qs,out signals, we conclude that terraces, floodplains, and the channel itself act as a temporary storage space where sediment can be deposited or remobilized when boundary conditions change (van den Berg van Saparoea and Postma, 2008; Coulthard et al., 2005; Simpson and Castelltort, 2012). The consequence of sediment deposition or remobilization during transient response times is that Qs,in differs from Qs,out, such that the Qs signal can be considered to be modified during transient phases of channel adjustment. Our data also support earlier findings by Simpson and Castelltort (2012) and van den Berg van Saparoea and Postma (2008), who concluded from their respective numerical model and physical experiments that Qw variability creates an amplified, substantial response in Qs,out, whereas changes in Qs,in create a dampened response in Qs,out due to a negative feedback between Qs,in and channel slope. Our experiments, illustrated schematically in Fig. 8, also suggest that Qw-driven Qs,out changes are temporary and that as the channel slope adjusts to the new input Qw, Qs,out evolves back to its initial steady-state value. In contrast, Qs,out changes driven by variability in Qs,in may not be observable during transient channel adjustment but will occur and persist once the channel has adjusted to new steady-state conditions.
4.3 Combining the records
Both fill terraces in the transfer zone and changes in sedimentation rates in the deposition zone record changes in boundary conditions. Our experiments provide an opportunity to investigate the links between terrace formation and sediment export to the deposition zone, as well as how both of these records, if available, can disambiguate changes in past Qs,in, Qw, or base level.
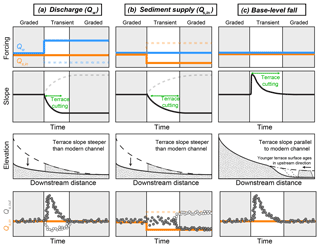
Figure 9Combining two records of landscape evolution to overcome ambiguity – terraces in the transfer zone and sediment discharge to the deposition zone (Qs,out) as a proxy for sedimentation rate. (a) The presence of terraces whose slopes differ from that of the main channel, combined with a simultaneous but transient peak in Qs,out, points towards Qw as the main driver of long-profile evolution. (b) The presence of terraces with steeper slopes compared to the modern channel combined with no immediate peak but an eventual reduction in Qs,out points towards Qs,in as the main driver. (c) A temporary increase in Qs,out combined with terraces that parallel the modern channel profile and become younger in the upstream direction indicates past changes in base level.
Sediment discharge at the outlet (Qs,out) is a function of (1) upstream sediment supply (Qs,in) and (2) sediment deposition or mobilization within the transfer zone. Doubling Qw while holding Qs,in constant triggers river incision to archive a lower channel slope (Fig. 9a). This incision leaves behind terraces that are steeper than the modern, graded channel. The sediment mobilized in the transfer zone during the transient incision phase produces a transient peak in Qs,out. Reducing Qs,in also reduces the equilibrium transport slope, causing channel incision and terrace abandonment (Fig. 9b). However, no peak in Qs,out during the transient phase is visible, as the extra sediment remobilized from the transfer zone is compensated for by the preceding reduction in Qs,in. Finally, incision due to a fall in base level also generates a temporary peak in Qs,out due to the additional sediment remobilized within the transfer zone (Fig. 9c). The terraces left behind following this base-level-driven incision, however, have slopes parallel to that of the modern, graded channel. In summary, Qs,out reflects a combination of Qs,in and the geometrical adjustment of the transfer zone, which in turn is recorded by fill terraces.
Coupling the two records, if available, provides the opportunity to unambiguously identify the forcing mechanism, which is not possible using either the fill terraces or the deposits alone (Fig. 9). For example, the presence of terraces whose slopes are steeper than the present-day channel, combined with a simultaneous but transient peak in Qs,out, points towards a change in Qw as the main driver. In turn, terraces whose slopes are steeper than the main channel in combination with a lagged reduction in Qs,out point towards a change in Qs,in as the main driver. Finally, a temporary increase in Qs,out in combination with channel-parallel terraces that young in the upstream direction indicates past base-level fall. Complications may arise when the forcing includes a combination of changes in Qs,in and Qw. Nevertheless, our results point to the potential of combining terrace records with sediment-export data for the reconstructions of paleoenvironmental conditions.
4.4 Limitations of experiments
Physical experiments allow for investigations of the isolated influence of individual key parameters on landscape evolution. However, a number of limitations arise when attempting to compare the experimental results to natural settings.
First of all, in natural sediment-routing systems, the three distinct zones of erosion, transfer, and deposition (Fig. 1) are coupled to one another (Allen, 2017). Erosion processes on the hillslopes, for example, determine the amount of sediment provided to the transfer zone, i.e., Qs,in (e.g., Dixon et al., 2009; Tofelde et al., 2018). In turn, changes in channel-bed elevation in the transfer zone can affect hillslope-erosion processes (e.g., Hurst et al., 2012; Roering et al., 2007). In our experimental setup, however, we investigate the response of the transfer zone as an isolated feature and can thus not account for any hillslope–channel feedbacks that might lead to additional variations in sediment supply to the channel.
Second, we varied Qw and Qs,in separately, forcing them to remain independent of one another. In natural systems, however, they are commonly coupled. For example, changes in precipitation can alter both Qw and Qs,in – directly though changes in rainfall-driven sediment-transport rates from hillslopes to the channel (Bookhagen et al., 2006; Dey et al., 2016; Steffen et al., 2009, 2010) and indirectly through long-term changes in hillslope-stabilizing vegetation types (Garcin et al., 2017; Langbein and Schumm, 1958; Schmid et al., 2018; Torres Acosta et al., 2015; Werner et al., 2018). Those feedback mechanisms between different key parameters (Qw, Qs,in) and between subzones of sediment-routing systems will likely complicate the forcing-response behavior of natural systems.
Third, we have only investigated a single, braided channel. Therefore, our experimental setup does not allow us to investigate channel-geometry adjustments related to feedbacks between the main stem and adjacent tributaries (Schumm, 1973, 1979), as well as related terraces forming at channel junctions (Faulkner et al., 2016; Larson et al., 2015; Schildgen et al., 2016). Furthermore, we can draw no conclusions on terraces forming in meandering rivers, such as those related to meander-bend cutoff (e.g., Erkens et al., 2009; Gonzalez, 2001; Limaye and Lamb, 2016). As such, the lack of terrace formation in the two control experiments after the spin-up time does not imply that autogenic terraces do not exist in natural systems, because several potential mechanisms of autogenic or complex-response terrace formation like meander-bend cutoff (Erkens et al., 2009; Gonzalez, 2001; Limaye and Lamb, 2016; Womack and Schumm, 1977) or internal feedbacks between the main stem and tributaries (Schumm, 1979, 1973; Gardener, 1983; Schumm and Parker, 1973; Slingerland and Snow, 1988) could not be tested with our experimental setup.
Fourth, apart from the step changes in input parameters, Qs,in and Qw were held constant through time. As the experiments exhibit geomorphically effective flow conditions at all times (intermittency equals 1), we assume that the experiments integrate over a number of large floods in natural channels. Natural rivers, in turn, experience a wide range of intermittencies. This variability in natural systems complicates any attempts to scale channel response times and lag times from experiments to real systems, but it also complicates the comparison of real systems with each other.
Finally, we performed a limited number of experimental runs, with only the control experiments being repeated. Although we did not repeat the experiments that included external perturbations, we consider the last phase of the two experiments during which we performed two changes (DQw_IQw and ) as repetition of the experiments with only one perturbation (IQw and DQs,in), albeit with different absolute values of Qw and Qs,in. Comparing those experiments reveals similar trajectories of channel evolution (longitudinal profiles, slope, width; Figs. 5 and 6). In addition, the same boundary conditions () persisted during the spin-up phases as well as at the end of the two experiments during which we performed two changes. During those conditions, the channel slopes always evolved to a value of ∼0.07. Although they are not exact repetitions of the same experiments, the evolution to the same equilibrium conditions indicates that the results are reproducible. But we acknowledge that further repetitions would improve our ability to quantify variability that is internal to each system.
Despite the above limitations, the performance of physical experiments under controlled conditions allows us to directly link causes and their effects in fluvial systems. As the key parameters (Qs,in, Qw, base level) can be varied independently, physical experiments provide the opportunity to isolate the influence of different environmental parameters on the evolution of landscapes and to test theoretical models (Paola et al., 2001). As many processes acting in landscapes are scale-independent, experimental observations can help to decipher process behavior in natural systems (e.g., Cantelli et al., 2004).
4.5 Implications for field studies
Despite the restrictions when comparing the experimental work to natural systems, the general patterns that we observed do have implications for field studies. First, lag times between the perturbation and the onset of terrace cutting can be important when dating the surfaces of fluvial–fill terraces in the field. Common methods to date the onset of river incision include the dating of terrace-surface material with cosmogenic exposure dating (e.g., Schildgen et al., 2016; Tofelde et al., 2017), dating sand or silt lenses with optically stimulated luminescence close to the terrace surface (OSL; e.g., Fuller et al., 1998; Schildgen et al., 2016; Steffen et al., 2009), or dating embedded organic material with 14C (Farabaugh and Rigsby, 2005; Scherler et al., 2015). When transferring our observations to a field scenario, the ∼2 h or more of channel material reworking before terraces were cut within the upstream part of the channel in the BLF and the DQs,in experiment would result in terrace ages that are younger than the time of perturbation. The best temporal correlations between the perturbation and the terrace-surface ages are achieved by those formed by changes in Qw due to the fast onset of vertical incision and minimal reworking of terrace-surface material. To assess the significance of this time lag in natural systems requires more work on how to scale the experiment to larger channels.
Second, in tectonically active regions, both strath and fill terraces have been used to calculate river incision rates to infer tectonic uplift rates (e.g., Litchfield and Berryman, 2006; Maddy et al., 2001; Schildgen et al., 2012; Wegmann and Pazzaglia, 2009). Because the slope changed in our experiments of upstream perturbations, incision rates were not uniform along the channel (Fig. 5). Litchfield and Berryman (2006) also measured variable fluvial incision rates based on terrace heights at several locations along 10 major rivers located along the Hikurangi Margin, New Zealand. Accordingly, incision rates reconstructed from terraces should be interpreted in the context of potential changes to the shape of the longitudinal profile in addition to tectonic changes.
Third, despite information stored in variable sediment deposition rates in the transfer or deposition zone, information on landscape evolution can also be preserved in the chemical composition of the deposited sediment. Our findings have implications for geochemical signatures of sediment, for example the concentration of cosmogenic 10Be, which is commonly measured to infer catchment mean denudation rates (Bierman and Steig, 1996; Brown et al., 1995; Granger et al., 1996). In cases of channel aggradation, Qs,out is reduced compared to Qs,in due to deposition within the channel (Fig. 8b, d, f). The exported sediment could be sourced from incoming sediment that is not deposited (grey circles) and/or mixes with remobilized sediment within the channel (yellow circles). In general, net deposition along the channel leads to the majority of the grains at the outlet being freshly delivered from local hillslopes, thus carrying the contemporaneous catchment chemical composition at the time of transport. In contrast, during incision, older material stored within the channel, floodplain, and/or terraces is remobilized and contributes to the temporary enhancement of Qs,out compared to Qs,in (Fig. 8a, c, e). Shortly after the perturbation, most of the remobilized sediment will be stratigraphically high and relatively young (yellow circles), but older material from deeper layers (orange and red circles) will be progressively remobilized and mixed with young material from upstream. Cosmogenic nuclide analyses along the eastern Altiplano margin (Hippe et al., 2012) and in the Amazon basin (Wittmann et al., 2011) indicate that sediment can be stored within the fluvial system over thousands to millions of years. Remobilization of formerly deposited material and subsequent mixing with fresh hillslope material (incoming sediment) can temporally modify signals stored in the geochemical composition of detrital river sediments (e.g., Tofelde et al., 2018; Wittmann et al., 2016, 2011). The degree of modification is thought to be a function of the ratio between fresh and remobilized material exported at a certain time as well as of the difference in geochemical composition between the fresh and remobilized material. We conclude that modern chemical signals are more likely to be transmitted through the system during aggradation phases, whereas local sediment that has been transiently stored may strongly overprint the signal of modern sediments during times of incision.
We performed seven physical experiments to investigate the effects of changing boundary conditions (, base level) on channel geometry and related fill-terrace cutting as well as on sediment discharge (Qs,out). To reliably reconstruct paleoenvironmental conditions from terraces in the transfer zone or sedimentary deposits in the sedimentation zone, it is important to understand (1) how information on environmental conditions may be modified and eventually transferred into the geologic record and (2) whether the geomorphic characteristics of terraces or the patterns of sedimentation rates are specific to the forcing mechanism.
Our experiments provide important insights into the coupling between sediment discharge to the deposition zone (Qs,out) and terrace formation in the transfer zone. Sediment discharge to the deposition zone (Qs,out) is a combination of sediment supply to the transfer zone (Qs,in) and its modification within the transfer zone through deposition or remobilization. Deposition or remobilization of sediment within the transfer zone occurs mainly during the transient response phase after a perturbation. Hence, during the transient response, Qs,out does not equal Qs,in. One consequence of this finding for field studies is that the geochemical composition of sediment sampled during transient river incision does not represent direct hillslope inputs alone but rather includes a significant component of remobilized sediment from some point in the geologic past. This remobilization can modify the 10Be concentration in detrital sediment, thus impacting estimates of catchment-wide denudation rates.
The same modifications (sediment deposition and remobilization) that alter the Qs signal during transient times also form fill terraces in the transfer zone. Increases in Qw trigger channel incision to archive a lower equilibrium slope. The resulting temporary peak in Qs,out coincides with the cutting of terraces whose slopes are steeper than the main channel. Reducing Qs,in also reduces the equilibrium transport slope, causing channel incision and terrace abandonment. However, no substantial increase in Qs,out occurs during the transient phase, as the extra sediment remobilized from the transfer zone is compensated for by the preceding reduction in Qs,in. Finally, a drop in base level causes a temporary peak in Qs,out and the formation of terraces parallel to the modern channel.
If both terrace and depositional records are available, the combination of the two can unambiguously identify the main mechanism driving channel adjustment. Identifying this mechanism can be important, for example, when using the height of terraces to infer channel incision rates. As upstream perturbations cause greater incision at the upstream end than at the downstream end, incision rates inferred from terrace heights are expected to vary along the profile.
The cutting of terraces following an upstream perturbation (Qs,in, Qw) requires a period of time (lag time) that is a function of incision rate, which in turn is expected to be a function of the excess transport capacity of a channel (Wickert and Schildgen, 2019). Indeed, our experiments showed that greater excess transport capacity leads to faster incision and shorter lag times, thus ensuring better preservation of the channel profile that existed prior to perturbation. These lag times can also be critical for field studies that attempt to link the ages of terraces surfaces to the timing of perturbations, as long lag times may lead to substantial temporal mismatches between forcing and fluvial-system response.
Topographic data from laser scans, overhead photographs, time-lapse movies, and experiment documentation have been published through the Sediment Experimentalists Network Project Space to the SEAD Internal Repository (Tofelde et al., 2019) and can be accessed through https://doi.org/10.26009/s0ZYPUYN.
The supplement related to this article is available online at: https://doi.org/10.5194/esurf-7-609-2019-supplement.
ST, SS, and ADW designed and built the experimental setup. ST and SS performed the experiments. ST analyzed the data with the help of SS, ADW and AB. All authors discussed the data, designed the manuscript, and commented on it. ST designed the artwork.
The authors declare that they have no conflict of interest.
We thank Ben Erickson, Richard Christopher, Chris Ellis, Jim Mullin, and Eric Steen for their help in building the experimental setup and installing equipment. We are also thankful to Jean-Louis Grimaud and Chris Paola for fruitful discussions and suggestions. We thank Luca Malatesta and two anonymous reviewers for their constructive feedback that improved the manuscript.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. SCHI 1241/1-1), the Alexander von Humboldt-Stiftung (grant no. ITA 1154030 STP), and the University of Minnesota.
This paper was edited by Sebastien Castelltort and reviewed by Luca C. Malatesta and two anonymous referees.
Allen, P. A.: From landscapes into geological history, Nature, 451, 274–276, https://doi.org/10.1038/nature06586, 2008.
Allen, P. A.: Sediment routing systems: The fate of sediment from source to sink, Cambridge University Press, Cambridge, UK and New York, USA, https://doi.org/10.1017/9781316135754, 2017.
Allen, P. A. and Densmore, A. L.: Sediment flux from an uplifting fault block, Basin Res., 12, 367–380, https://doi.org/10.1046/j.1365-2117.2000.00135.x, 2000.
Alloway, B. V., Lowe, D. J., Barrell, D. J. A., Newnham, R. M., Almond, P. C., Augustinus, P. C., Bertler, N. A. N., Carter, L., Litchfield, N. J., Mcglone, M. S., Shulmeister, J., Vandergoes, M. J., Williams, P. W., and Members, N.-I.: Towards a climate event stratigraphy for New Zealand over the past 30 000 years (NZ-INTIMATE project), J. Quaternary Sci., 22, 9–35, https://doi.org/10.1002/jqs.1079, 2007.
Armitage, J. J., Duller, R. A., Whittaker, A. C., and Allen, P. A.: Transformation of tectonic and climatic signals from source to sedimentary archive, Nat. Geosci., 4, 231–235, 2011.
Armitage, J. J., Dunkley Jones, T., Duller, R. A., Whittaker, A. C., and Allen, P. A.: Temporal buffering of climate-driven sediment flux cycles by transient catchment response, Earth Planet. Sc. Lett., 369–370, 200–210, https://doi.org/10.1016/j.epsl.2013.03.020, 2013.
Baynes, E. R. C., Lague, D., and Kermarrec, J.: Supercritical river terraces generated by hydraulic and geomorphic interactions, Geology, 46, 1–4, https://doi.org/10.1130/G40071.1, 2018.
Begin, Z. B., Meyer, D. F., and Schumm, S. A.: Development of longitudinal profiles of alluvial channels in response to base-level lowering, Earth Surf. Proc. Land., 6, 49–68, 1981.
Bierman, P. and Steig, E. J.: Estimating rates of denudation using cosmogenic isotope abundances in sediment, Earth Surf. Proc. Land., 21, 125–139, https://doi.org/10.1002/(SICI)1096-9837(199602)21:2<125::AID-ESP511>3.0.CO;2-8, 1996.
Blom, A., Viparelli, E., and Chavarrías, V.: The graded alluvial river: Profile concavity and downstream fining, Geophys. Res. Lett, 43, 6285–6293, https://doi.org/10.1002/2016GL068898, 2016.
Blom, A., Arkesteijn, L., Chavarrias, V., and Viparelli, E.: The equilibrium alluvial river under variable flow and its channel-forming discharge, J. Geophys. Res.-Earth, 122, 1924–1948, https://doi.org/10.1002/2017JF004213, 2017.
Blum, M. D. and Tornqvist, T. E.: Fluvial responses to climate and sea-level change: a review and look forward, Sedimentology, 47, 2–48, https://doi.org/10.1046/j.1365-3091.2000.00008.x, 2000.
Bonnet, S. and Crave, A.: Landscape response to climate change: Insights from experimental modeling and implications for tectonic versus climatic uplift of topography, Geology, 31, 123–126, 2003.
Bookhagen, B., Fleitmann, D., Nishiizumi, K., Strecker, M. R., and Thiede, R. C.: Holocene monsoonal dynamics and fluvial terrace formation in the northwest Himalaya, India, Geology, 34, 601–604, https://doi.org/10.1130/G22698.1, 2006.
Bridgland, D. and Westaway, R.: Climatically controlled river terrace staircases: a worlwide Quaternary phenomenon, Geomorphology, 98, 285–315, 2008.
Brown, E. T., Stallard, R. F., Larsen, M. C., Raisbeck, G. M., and Yiou, F.: Denudation rates determined from the accumulation of in situ-produced 10Be in the Luquillo Experimental Forest, Puerto Rico, Earth Planet. Sc. Lett., 129, 193–202, https://doi.org/10.1016/0012-821X(94)00249-X, 1995.
Bufe, A., Turowski, J. M., Burbank, D. W., Paola, C., Wickert, A. D., and Tofelde, S.: Controls on lateral channel mobility and the reworked area of active alluvial surfaces, in: EGU General Assembly Conference Abstracts, 8–13 April 2018, Vienna, Austria, p. 13437, 2018.
Buffington, J. M.: Changes in channel morphology over human time scales, chap. 32, Gravel-Bed Rivers Processes, Tools, Environments, edited by: Church, M., Biron, P. M., and Roy, A. G., Wiley, Chichester, UK, 435–463, 2012.
Bull, W. B.: Stream-terrace genesis: implications for soil development, Geomorphology, 3, 351–367, https://doi.org/10.1016/0169-555X(90)90011-E, 1990.
Bull, W. B.: Geomorphic responses to climatic change, Oxford University Press, USA, 1991.
Cantelli, A., Paola, C., and Parker, G.: Experiments on upstream-migrating erosional narrowing and widening of an incisional channel caused by dam removal, Water Resour. Res., 40, W03304, https://doi.org/10.1029/2003WR002940, 2004.
Castelltort, S. and Van Den Driessche, J.: How plausible are high-frequency sediment supply-driven cycles in the stratigraphic record?, Sediment. Geol., 157, 3–13, https://doi.org/10.1016/S0037-0738(03)00066-6, 2003.
Coulthard, T. J. T., Lewin, J., and Macklin, M. G.: Modelling differential catchment response to environmental change, Geomorphology, 69, 222–241, https://doi.org/10.1016/j.geomorph.2005.01.008, 2005.
Dey, S., Thiede, R. C., Schildgen, T. F., Wittmann, H., Bookhagen, B., Scherler, D., Jain, V., and Strecker, M. R.: Climate-driven sediment aggradation and incision since the late Pleistocene in the NW Himalaya, India, Earth Planet. Sc. Lett., 449, 321–331, https://doi.org/10.1016/j.epsl.2016.05.050, 2016.
Dixon, J. L., Heimsath, A. M., Kaste, J., and Amundson, R.: Climate-driven processes of hillslope weathering, Geology, 37, 975–978, https://doi.org/10.1130/G30045A.1, 2009.
Erkens, G., Dambeck, R., Volleberg, K. P., Bouman, M. T. I. J., Bos, J. A. A., Cohen, K. M., Wallinga, J., and Hoek, W. Z.: Fluvial terrace formation in the northern Upper Rhine Graben during the last 20,000 years as a result of allogenic controls and autogenic evolution, Geomorphology, 103, 476–495, https://doi.org/10.1016/j.geomorph.2008.07.021, 2009.
Farabaugh, R. L. and Rigsby, C. A.: Climatic influence on sedimentology and geomorphology of the Rio Ramis valley, Peru, J. Sediment. Res., 75, 12–28, 2005.
Faulkner, D. J., Larson, P. H., Jol, H. M., Running, G. L., Loope, H. M., and Goble, R. J.: Autogenic incision and terrace formation resulting from abrupt late-glacial base-level fall, lower Chippewa River, Wisconsin, USA, Geomorphology, 266, 75–95, https://doi.org/10.1016/j.geomorph.2016.04.016, 2016.
Fisk, N. H.: Geological investigation of the alluvial valley of the lower Mississippi River, Mississippi River Commission Print, Vicksburg, Mississippi, USA, 1944.
Frankel, K. L., Pazzaglia, F. J., and Vaughn, J. D.: Knickpoint evolution in a vertically bedded substrate, upstream-dipping terraces, and Atlantic slope bedrock channels, GSA Bull., 119, 476–486, https://doi.org/10.1130/B25965.1, 2007.
Fuller, I. C., Macklin, M. G., Lewin, J., Passmore, D. G., and Wintle, A. G.: River response to high-frequency climate oscillations in southern Europe over the past 200 ky, Geology, 26, 275–278, https://doi.org/10.1130/0091-7613(1998)026<0275:RRTHFC>2.3.CO;2, 1998.
Garcin, Y., Schildgen, T. F., Torres Acosta, V., Melnick, D., Guillemoteau, J., Willenbring, J., and Strecker, M. R.: Short-lived increase in erosion during the African Humid Period: Evidence from the northern Kenya Rift, Earth Planet. Sc. Lett., 459, 58–69, https://doi.org/10.1016/j.epsl.2016.11.017, 2017.
Gardner, T. W.: Experimental study of knickpoint and longitudinal profile evolution in cohesive, homogeneous material, Geol. Soc. Am. Bull, 94, 664–572, https://doi.org/10.1130/0016-7606(1983)94<664:ESOKAL>2.0.CO;2, 1983.
Gilbert, G. K.: Report on the Geology of the Henry Mountains, US Gov. Print. Off., Washington, D.C., USA, https://doi.org/10.3133/70038096, 1877.
Godard, V., Tucker, G. E., Burch Fisher, G., Burbank, D. W., and Bookhagen, B.: Frequency-dependent landscape response to climatic forcing, Geophys. Res. Lett., 40, 859–863, https://doi.org/10.1002/grl.50253, 2013.
Gonzalez, M. A.: Recent formation of arroyos in the Little Missouri Badlands of southwestern North Dakota, Geomorphology, 38, 63–84, 2001.
Granger, D. E., Kirchner, J. W., and Finkel, R.: Spatially averaged long-term erosion rates measured from in situ-produced cosmogenic nuclides in alluvial sediment, J. Geol., 104, 249–257, 1996.
Hanson, P. R., Mason, J. A., and Goble, R. J.: Fluvial terrace formation along Wyoming's Laramie Range as a response to increased late Pleistocene flood magnitudes, Geomorphology, 76, 12–25, https://doi.org/10.1016/j.geomorph.2005.08.010, 2006.
Hardy, D. R., Bradley, R. S., and Zolitschka, B.: The climatic signal in varved sediments from Lake C2, northern Ellesmere Island, Canada, J. Paleolimnol., 16, 227–238, https://doi.org/10.1007/BF00176938, 1996.
Hippe, K., Kober, F., Zeilinger, G., Ivy-ochs, S., Maden, C., Wacker, L., Kubik, P. W., and Wieler, R.: Quantifying denudation rates and sediment storage on the eastern Altiplano, Bolivia, using cosmogenic 10Be, 26Al, and in situ 14C, Geomorphology, 179, 58–70, https://doi.org/10.1016/j.geomorph.2012.07.031, 2012.
Howard, A. D.: Numerical systems of terrace nomenclature: A critique, J. Geol., 67, 239–243, 1959.
Howard, A. D.: Equilibrium and time scales in geomorphology: Application to sand-bed alluvial streams, Earth Surf. Proc. Land., 7, 303–325, 1982.
Huntington, E.: Some characteristics of the glacial period in non-glaciated region, Bull. Geol. Soc. Am., 18, 351–388, 1907.
Hurst, M. D., Mudd, S. M., Walcott, R., Attal, M., and Yoo, K.: Using hilltop curvature to derive the spatial distribution of erosion rates, J. Geophys. Res.-Earth, 117, 1–19, https://doi.org/10.1029/2011JF002057, 2012.
Lane, E. W.: Importance of fluvial morphology in hydraulic engineering, Proceedings of the American Society of Civil Engineers, 81, 1–17, 1955.
Langbein, W. B. and Schumm, S. A.: Yield of sediment in relation to mean annual precipitation, EOS T. Am. Geophys. Un., 39, 1076–1084, 1958.
Larson, P. H., Dorn, R. I., Faulkner, D. J., and Friend, D. A.: Toe-cut terraces: A review and proposed criteria to differentiate from traditional fluvial terraces, Prog. Phys. Geogr., 39, 417–439, 2015.
Lewis, W. V.: Stream trough experiments and terrace formation, Geol. Mag., 81, 241–253, 1944.
Limaye, A. B. S. and Lamb, M. P.: Numerical model predictions of autogenic fluvial terraces and comparison to climate change expectations, J. Geophys. Res.-Earth, 121, 512–544, https://doi.org/10.1002/2014JF003392, 2016.
Litchfield, N. and Berryman, K.: Relations between postglacial fluvial incision rates and uplift rates in the North Island, New Zealand, J. Geophys. Res., 111, 1–15, https://doi.org/10.1029/2005JF000374, 2006.
Litty, C., Duller, R., and Schlunegger, F.: Paleohydraulic reconstruction of a 40 ka-old terrace sequence implies that water discharge was larger than today, Earth Surf. Proc. Land., 41, 884–898, https://doi.org/10.1002/esp.3872, 2016.
Mackin, J. H.: Concept of the graded river, Bull. Geol. Soc. Am., 59, 463–512, 1948.
Maddy, D., Bridgland, D., and Westaway, R.: Uplift-driven valley incision and climate-controlled river terrace development in the Thames Valley, UK, Quatern. Int., 79, 23–36, 2001.
Malatesta, L. C. and Avouac, J.: Contrasting river incision in north and south Tian Shan piedmonts due to variable glacial imprint in mountain valleys, Geology, 46, 659–662, 2018.
Malatesta, L. C. and Lamb, M. P.: Formation of waterfalls by intermittent burial of active faults, GSA Bull., 130, 522–536, 2018.
Malatesta, L. C., Prancevic, J. P., and Avouac, J.: Autogenic entrenchment patterns and terraces due to coupling with lateral erosion in incising alluvial channels, J. Geophys. Res.-Earth, 122, 335–355, https://doi.org/10.1002/2015JF003797, 2017.
Malatesta, L., Avouac, J.-P., Brown, N. D., Breitenbach, S. F. M., Pan, J., Chevalier, M.-L., Rhodes, E., Saint-Carlier, D., Zhang, W., Charreau, J., Lavé, J., and Blard, P.-H.: Lag and mixing during sediment transfer across the Tian Shan piedmont caused by climate- driven aggradation-incision cycles, Basin Res., 30, 613–635, https://doi.org/10.1111/bre.12267, 2018.
McPhillips, D., Bierman, P. R., and Rood, D. H.: Millennial-scale record of landslides in the Andes consistent with earthquake trigger, Nat. Geosci., 7, 925–930, 2014.
Merritts, D. J., Vincent, K. R., and Wohl, E. E.: Long river profiles, tectonism, and eustasy: A guide to interpreting fluvial terraces, J. Geophys. Res., 99, 14031–14050, 1994.
Métivier, F. and Gaudemer, Y.: Stability of output fluxes of large rivers in South and East Asia during the last 2 million years?: implications on floodplain processes, Basin Res., 11, 293–303, 1999.
Meyer-Peter, E. and Müller, R.: Formulas for Bed-Load Transport, in: 2nd Meeting of the International Association for Hydraulic Structures Research, 7–9 June 1948, Stockholm, Sweden, International Association for Hydraulic Structures Research, 39–64, 1948.
Mizutani, T.: Laboratory experiment and digital simulation of multiple fill-cut terrace formation, Geomorphology, 24, 353–361, https://doi.org/10.1016/S0169-555X(98)00027-0, 1998.
Norton, K. P., Schlunegger, F., and Litty, C.: On the potential for regolith control of fluvial terrace formation in semi-arid escarpments, Earth Surf. Dynam., 4, 147–157, https://doi.org/10.5194/esurf-4-147-2016, 2016.
Paola, C., Heller, P. L., and Angevine, C. L.: The large-scale dynamics of grain-size variation in alluvial basins, 1: Theory, Basin Res., 4, 73–90, https://doi.org/10.1111/j.1365-2117.1992.tb00145.x, 1992.
Paola, C., Mullin, J., Ellis, C., Mohrig, D. C., Swenson, J. B., Parker, G., Hickson, T., Heller, P. L., Pratson, L., and Syvitski, J.: Experimental stratigraphy, GSA Today, 11, 4–9, 2001.
Parker, G.: Hydraulic geometry of active gravel rivers, J. Hydraul. Div., 105, 1185–1201, 1979.
Patton, P. C. and Schumm, S. A.: Ephemeral-Stream Processes: Implications for Studies of Quaternary Valley Fills, Quaternary Res., 15, 24–43, 1981.
Pazzaglia, F. J.: 9.23 Fluvial terraces, in: Treatise of Geomorphology, edited by: Wohl, E., Elsevier, Amsterdam, the Netherlands, 379–-412, 2013.
Pederson, J. L., Anders, M. D., Rittenhour, T. M., Sharp, W. D., Gosse, J. C., and Karlstrom, K. E.: Using fill terraces to understand incision rates and evolution of the Colorado River in eastern Grand Canyon, Arizona, J. Geophys. Res., 111, F02003, https://doi.org/10.1029/2004JF000201, 2006.
Penck, A. and Brückner, E.: Die Alpen im Eiszeitalter, Tauchnitz, Leipzig, Germany, 1909.
Pepin, E., Carretier, S., Hérail, G., Regard, V., Charrier, R., Farías, M., García, V., and Giambiagi, L.: Pleistocene landscape entrenchment: a geomorphological mountain to foreland field case, the Las Tunas system, Argentina, Basin Res., 25, 613–637, 2013.
Poisson, B. and Avouac, J. P.: Holocene Hydrological Changes Inferred from Alluvial Stream Entrenchment in North Tian Shan (Northwestern China), J. Geol., 112, 231–249, 2004.
Roering, J. J., Perron, J. T., and Kirchner, J. W.: Functional relationships between denudation and hillslope form and relief, Earth Planet. Sc. Lett., 264, 245–258, https://doi.org/10.1016/j.epsl.2007.09.035, 2007.
Romans, B. W., Castelltort, S., Covault, J. A., Fildani, A., and Walsh, J. P.: Environmental signal propagation in sedimentary systems across timescales, Earth-Sci. Rev., 153, 7–29, https://doi.org/10.1016/j.earscirev.2015.07.012, 2016.
Savi, S., Norton, K. P., Picotti, V., Akçar, N., Delunel, R., Brardinoni, F., Kubik, P., and Schlunegger, F.: Quantifying sediment supply at the end of the last glaciation: Dynamic reconstruction of an alpine debris-flow fan, GSA Bull., 126, 773–790, https://doi.org/10.1130/B30849.1, 2014.
Savi, S., Delunel, R., and Schlunegger, F.: Efficiency of frost-cracking processes through space and time: An example from the eastern Italian Alps, Geomorphology, 232, 248–260, https://doi.org/10.1016/j.geomorph.2015.01.009, 2015.
Schaller, M., von Blanckenburg, F., Hovius, N., Veldkamp, A., van den Berg, M. W., and Kubik, P. W.: Paleoerosion rates from cosmogenic 10Be in a 1.3 Ma terrace sequence: Response of the River Meuse to changes in climate and rock uplift, J. Geol., 112, 127–144, 2004.
Scherler, D., Bookhagen, B., Wulf, H., Preusser, F., and Strecker, M. R.: Increased late Pleistocene erosion rates during fluvial aggradation in the Garhwal Himalaya , northern India, Earth Planet. Sc. Lett., 428, 255–266, https://doi.org/10.1016/j.epsl.2015.06.034, 2015.
Scherler, D., Lamb, M. P., Rhodes, E. J., and Avouac, J. P.: Climate-change versus landslide origin of fill terraces in a rapidly eroding bedrock landscape: San Gabriel River, California, Bull. Geol. Soc. Am., 128, 1228–1248, https://doi.org/10.1130/B31356.1, 2016.
Schildgen, T., Dethier, D. P., Bierman, P., and Caffee, M.: 26Al and 10Be dating of Late Pleistocene and Holocene fill terraces: A record of fluvial deposition and incision, Colorado Front Range, Earth Surf. Proc. Land., 27, 773–787, https://doi.org/10.1002/esp.352, 2002.
Schildgen, T. F., Cosentino, D., Bookhagen, B., Niedermann, S., Yildirim, C., Echtler, H., Wittmann, H., and Strecker, M. R.: Multi-phased uplift of the southern margin of the Central Anatolian plateau, Turkey: A record of tectonic and upper mantle processes, Earth Planet. Sc. Lett., 317–318, 85–95, https://doi.org/10.1016/j.epsl.2011.12.003, 2012.
Schildgen, T. F., Robinson, R. A. J., Savi, S., Phillips, W. M., Spencer, J. Q. G., Bookhagen, B., Scherler, D., Tofelde, S., Alonso, R. N., Kubik, P. W., Binnie, S. A., and Strecker, M. R.: Landscape response to late Pleistocene climate change in NW Argentina: Sediment flux modulated by basin geometry and connectivity, J. Geophys. Res.-Earth, 121, 392–414, https://doi.org/10.1002/2015JF003607, 2016.
Schmid, M., Ehlers, T. A., Werner, C., Hickler, T., and Fuentes-Espoz, J.-P.: Effect of changing vegetation and precipitation on denudation – Part 2: Predicted landscape response to transient climate and vegetation cover over millennial to million-year timescales, Earth Surf. Dynam., 6, 859–881, https://doi.org/10.5194/esurf-6-859-2018, 2018.
Schumm, S. A.: Geomorphic thresholds and complex response of drainage systems, Fluv. Geomorphol., 6, 69–85, 1973.
Schumm, S. A.: Geomorphic thresholds: the concept and its applications, R. Geogr. Soc., 4, 485–515, 1979.
Schumm, S. A. and Parker, R. S.: Implication of complex response of drainage systems for Quaternary alluvial stratigraphy, Nat. Phys. Sci., 243, 99–100, 1973.
Shen, Z., Törnqvist, T. E., Autin, W. J., Mateo, Z. R. P., Straub, K. M., and Mauz, B.: Rapid and widespread response of the Lower Mississippi River to eustatic forcing during the last glacial-interglacial cycle, GSA Bull., 124, 690–704, https://doi.org/10.1130/B30449.1, 2012.
Simpson, G. and Castelltort, S.: Model shows that rivers transmit high-frequency climate cycles to the sedimentary record, Geology, 40, 1131–1134, https://doi.org/10.1130/G33451.1, 2012.
Slingerland, R. L. and Snow, R. S.: Stability analysis of a rejuvenated fluvial system, Z. Geomorphol., 67, 93–102, 1988.
Steffen, D., Schlunegger, F., and Preusser, F.: Drainage basin response to climate change in the Pisco valley, Peru, Geology, 37, 491–494, 2009.
Steffen, D., Schlunegger, F., and Preusser, F.: Late Pleistocene fans and terraces in the Majes valley, southern Peru, and their relation to climatic variations, Int. J. Earth Sci., 99, 1975–1989, 2010.
Tebbens, L. A., Veldkamp, A., Van Dijke, J. J., and Schoorl, J. M.: Modeling longitudinal-profile development in response to Late Quaternary tectonics, climate and sea-level changes: the River Meuse, Global Planet. Change, 27, 165–186, 2000.
Tofelde, S., Schildgen, T. F., Savi, S., Pingel, H., Wickert, A. D., Bookhagen, B., Wittmann, H., Alonso, R. N., Cottle, J., and Strecker, M. R.: 100 kyr fluvial cut-and-fill terrace cycles since the Middle Pleistocene in the southern Central Andes, NW Argentina, Earth Planet. Sc. Lett., 473, 141–153, https://doi.org/10.1016/j.epsl.2017.06.001, 2017.
Tofelde, S., Duesing, W., Schildgen, T. F., Wickert, A. D., Wittmann, H., Alonso, R. N., and Strecker, M.: Effects of deep-seated versus shallow hillslope processes on cosmogenic 10Be concentrations in fluvial sand and gravel, Earth Surf. Proc. Land., 43, 3086–3098, 2018.
Tofelde, S., Savi, S., Wickert, A., Bufe, A., and Schildgen, T.: Physical experiments on fill-terrace formation and sediment-signal disruption, SEAD Internal Repository, https://doi.org/10.26009/s0ZYPUYN, 2019.
Torres Acosta, V., Schildgen, T. F., Clarke, B. A., Scherler, D., Bookhagen, B., Wittmann, H., von Blanckenburg, F., and Strecker, M. R.: Effect of vegetation cover on millennial-scale landscape denudation rates in East Africa, Lithosphere, 7, 408–420, https://doi.org/10.1130/L402.1, 2015.
Tucker, G. E. and Slingerland, R.: Drainage basin responses to climate change, Water Resour. Res., 33, 2031–2047, 1997.
Vandenberghe, J.: Timescales, climate and river development, Quaternary Sci. Rev., 14, 631–638, https://doi.org/10.1016/0277-3791(95)00043-O, 1995.
Vandenberghe, J.: Climate forcing of fluvial system development: An evolution of ideas, Quaternary Sci. Rev., 22, 2053–2060, https://doi.org/10.1016/S0277-3791(03)00213-0, 2003.
van den Berg van Saparoea, A.-P. H. and Postma, G.: Control of climate change on the yield of river systems, Recent Adv. Model. Siliciclastic Shallow-Marine Stratigr. SEPM Spec. Publ., 90, 15–33, 2008.
Wegmann, K. W. and Pazzaglia, F. J.: Late Quaternary fluvial terraces of the Romagna and Marche Apennines, Italy: Climatic, lithologic, and tectonic controls on terrace genesis in an active orogen, Quaternay Sci. Rev., 28, 137–165, https://doi.org/10.1016/j.quascirev.2008.10.006, 2009.
Werner, C., Schmid, M., Ehlers, T. A., Fuentes-Espoz, J. P., Steinkamp, J., Forrest, M., Liakka, J., Maldonado, A., and Hickler, T.: Effect of changing vegetation and precipitation on denudation – Part 1: Predicted vegetation composition and cover over the last 21 thousand years along the Coastal Cordillera of Chile, Earth Surf. Dynam., 6, 829–858, https://doi.org/10.5194/esurf-6-829-2018, 2018.
Wickert, A. D. and Schildgen, T. F.: Long-profile evolution of transport-limited gravel-bed rivers, Earth Surf. Dynam., 7, 17–43, https://doi.org/10.5194/esurf-7-17-2019, 2019.
Wickert, A. D., Martin, J. M., Tal, M., Kim, W., Sheets, B., and Paola, C.: River channel lateral mobility: Metrics, time scales, and controls, J. Geophys. Res.-Earth, 118, 396–412, https://doi.org/10.1029/2012JF002386, 2013.
Wittmann, H., von Blanckenburg, F., Maurice, L., Guyot, J. L., and Kubik, P. W.: Recycling of Amazon floodplain sediment quantified by cosmogenic 26Al and 10Be, Geology, 39, 467–470, https://doi.org/10.1130/G31829.1, 2011.
Wittmann, H., Malusà, M. G., Resentini, A., Garzanti, E., and Niedermann, S.: The cosmogenic record of mountain erosion transmitted across a foreland basin: source-to-sink analysis of in situ 10Be, 26Al and 21Ne in sediment of the Po river catchment, Earth Planet. Sc. Lett., 452, 258–271, https://doi.org/10.1016/j.epsl.2016.07.017, 2016.
Wobus, C. W., Tucker, G. E., and Anderson, R. S.: Does climate change create distinctive patterns of landscape incision?, J. Geophys. Res., 115, F04008, https://doi.org/10.1029/2009JF001562, 2010.
Wohl, E. and Ikeda, H.: Experimental simulation of channel incision into a cohesive substrate at varying gradients, Geology, 25, 295–298, 1997.
Womack, W. R. and Schumm, S. A.: Terraces of Douglas Creek, northwestern Colorado: An example of episodic erosion, Geology, 5, 72–76, https://doi.org/10.1130/0091-7613(1977)5<72:TODCNC>2.0.CO;2, 1977.
Zhang, P., Molnar, P., and Downs, W. R.: Increased sedimentation rates and grain sizes 2–4 Myr ago due to the influence of climate change on erosion rates, Nature, 410, 891–897, https://doi.org/10.1038/35073504, 2001.






