the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Displacement mechanisms of slow-moving landslides in response to changes in porewater pressure and dynamic stress
Jonathan M. Carey
Chris I. Massey
Barbara Lyndsell
David N. Petley
Although slow-moving landslides represent a substantial hazard, their detailed mechanisms are still comparatively poorly understood. We have conducted a suite of innovative laboratory experiments using novel equipment to simulate a range of porewater pressure and dynamic stress scenarios on samples collected from a slow-moving landslide complex in New Zealand. We have sought to understand how changes in porewater pressure and ground acceleration during earthquakes influence the movement patterns of slow-moving landslides. Our experiments show that during periods of elevated porewater pressure, displacement rates are influenced by two components: first an absolute stress state component (normal effective stress state) and second a transient stress state component (the rate of change of normal effective stress). During dynamic shear cycles, displacement rates are controlled by the extent to which the forces operating at the shear surface exceed the stress state at the yield acceleration point. The results indicate that during strong earthquake accelerations, strain will increase rapidly with relatively minor increases in the out-of-balance forces. Similar behaviour is seen for the generation of movement through increased porewater pressures. Our results show how the mechanisms of shear zone deformation control the movement patterns of large slow-moving translational landslides, and how they may be mobilised by strong earthquakes and significant rain events.
- Article
(3794 KB) - Full-text XML
- BibTeX
- EndNote
Landslides are a significant natural hazard, responsible for up to 14 000 fatalities per annum globally (Petley, 2012; Froude and Petley, 2018). Although most fatalities occur during high-velocity landslides, slow-moving landslides can cause high levels of loss. The movement of most non-seismic landslides is controlled by the effective stress state but the relationship between porewater pressure and ground movement in slow-moving landslides is more complex than is often appreciated (Petley et al., 2017). In a few instances a simple (albeit non-linear) relationship between porewater pressure and movement rate has been observed (e.g. Corominas et al., 1999) allowing reasonable predictions of movement rate for any given porewater pressure. Conversely, in many cases much more complex relationships have been observed (e.g. Skempton, 1985; Corominas et al., 2005; Gonzalez et al., 2008; Carey et al., 2016), often involving hysteresis, for reasons that are poorly understood.
To account for this complex behaviour, it has been proposed that shear-strength parameters, represented as c′ and ϕ′ in the Mohr–Coulomb failure criterion, can be modified by inclusion of a viscous resistance component (Bertini et al., 1984; Leroueil et al., 1996; Corominas et al., 2005; van Asch et al., 2007; Picarelli, 2007; Gonzalez et al., 2008). However, whilst the use of viscosity functions may improve our understanding and ability to predict patterns of landslide movement by assuming that once motion is triggered landslide displacement occurs as visco-plastic flow as opposed to frictional slip, such equations do not account for the porewater pressure and displacement hysteresis observed (e.g. Massey, 2010), requiring that the rate of movement reduces only when porewater pressures reduce. The observed hysteresis may be the result of a number of factors, including rate-induced changes in shear strength of the materials (e.g. Lupini et al., 1981; Skempton, 1985; Angeli et al., 1996; Picarelli, 2007; Petley et al., 2017) or consolidation or strength regain during periods of rest (e.g. Angeli et al., 2004).
Landslide movement triggered by dynamic stress changes (i.e. during earthquakes) can also be complex. Many hillslopes fail during large earthquakes, and recent landslide inventories (e.g. Li et al., 2014; Valagussa et al., 2016; Massey et al., 2018) illustrate that factors such as shaking intensity and hillslope proximity to fault are key proxies for drivers of landslide movement. Despite this, many hillslopes adjacent to slopes that fail show limited downslope deformation despite high levels of local ground shaking and similar material and topographic characteristics (Collins and Jibson, 2015; Petley et al., 2006). Similarly, the post-seismic behaviour of these damaged hillslopes is poorly understood (e.g. Keefer, 1994; Hovius et al., 2011).
High-quality measurement of earthquake-induced landslide movement is limited by the infrequency of high-magnitude seismic events and the challenges of collecting real-time landslide monitoring data over appropriate coseismic and interseismic timescales. Therefore, coseismic landslide displacement is most commonly assessed using numerical modelling approaches (e.g. the Newmark sliding model – see Jibson, 2011, for example) which treat landslides as rigid blocks capable of movement when downslope earthquake accelerations (based on acceleration time histories) exceed the basal frictional resistance (Newmark, 1965). These methods have provided reasonable estimates of earthquake-induced landside activity (e.g. Dreyfus et al., 2013) and are widely applied in regional landslide hazard assessments (e.g. Wilson and Keefer, 1983) but they provide little insight into the processes occurring at the shear surface.
Until today few laboratory-based studies have attempted to consider how porewater pressure changes and seismic excitation influence slow-moving landslide displacement rates. To do so requires field monitoring data of both high spatial resolution and high temporal resolution to parameterise the key factors and laboratory testing that accurately replicates the complex stress conditions within slopes, a combination that is rarely available.
In New Zealand, slow-moving landslides are abundant in soft sedimentary rocks. The financial costs associated with their on-going movement are significant, particularly in agricultural areas where mitigation measures or slope management practices are rarely implemented (Mcoll and McCabe, 2016). These sedimentary rocks mostly comprise Neogene fine-grained sandstones and mudstones, which cover approximately 17 % of New Zealand's land surface (Fig. 1a; Massey et al., 2016). The New Zealand Landslide Database contains approximately 7000 landslides within these sediments (Fig. 1b; Dellow et al., 2005; Rosser et al., 2017), the majority of which are relatively slow-moving, deep-seated, translational slides that reactivate frequently (Massey, 2010).
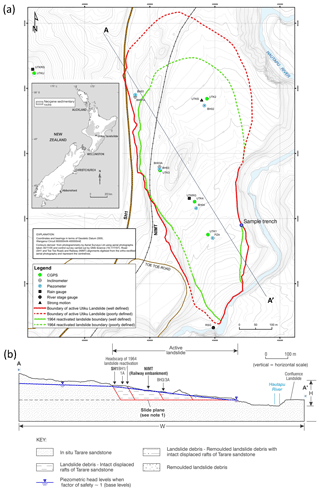
Figure 1(a) Location of the Utiku landslide in North Island, New Zealand, the location of monitoring equipment installed on the landslide in September 2008 and the location of the trench from which samples of the slide surface were taken. (b) Cross section A–A′ through the landslide, refer to panel (a) for the location of the section. Note 1: slide plane formed within a thin (10–20 mm) layer of smectite-rich clay.
In this study we present a suite of laboratory experiments that simulate a range of porewater-pressure and dynamic-stress scenarios on samples of smectite-rich clay taken from the slide surface of the Utiku landslide, a very large slow-moving slip. Such smectite-rich clays control many landslides in this area of New Zealand (Thompson, 1982; Massey, 2010). We compare the displacement patterns we observe in the laboratory to high-resolution monitoring records collected from the landslide – along with numerical modelling of (1) static stability, caused by changes in porewater pressure measured above the slide surface, and (2) dynamic stability, potential ground displacements caused by earthquakes – in order to get insights into the processes controlling the complex movement patterns observed in this landslide complex.
The Utiku landslide complex, formed of early to mid-Pliocene Tarare sandstone and Taihape mudstone (Lee et al., 2012; Massey et al., 2013), is located in the central part of North Island, New Zealand (location 39.75∘ S, 175.83∘ E; Fig. 1a). According to the Hungr et al. (2014) scheme, it is an active deep-seated translational or compound landslide with a volume of about 22×106 m3 (Massey et al., 2013). It has been studied since 1965, with high-resolution monitoring available since 2008. The landslide has generally moved slowly (varying between 16 mm yr−1 and 1.6 m yr−1; Stout, 1977) but it has repeatedly damaged the North Island Main Trunk railway (NIMT) and State Highway 1 (SH1), both of which cross the landslide (Fig. 1a and b).
2.1 Landslide displacements induced by porewater pressure increases
The Utiku landslide has been intensively studied using detailed field mapping, borehole analysis, evaluation of historical movements, and the analysis of data from piezometers, inclinometers and rain gauges (Massey, 2010). The displacement time series (Fig. 2a) reveals a complex behaviour dominated by periods of comparatively rapid movement, which can accumulate up to 120 mm of displacement per event at rates of up to 21 mm d−1 (Massey et al., 2013). These events coincide with seasonal peaks in porewater pressure (Fig. 2b), with movement primarily associated with basal sliding (Fig. 2c). While movement initiates with, and during periods of acceleration is controlled by, increases in porewater pressure, periods of deceleration are poorly correlated with porewater pressure value or any other monitored factor (Fig. 2d).
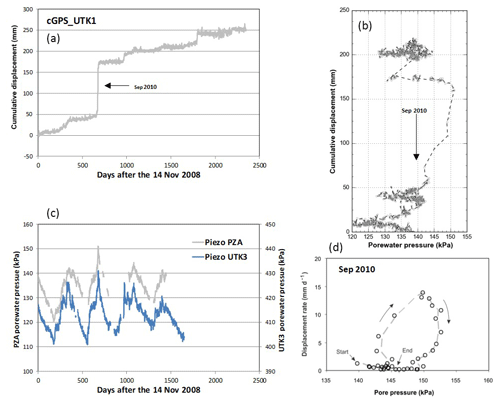
Figure 2Utiku landslide monitoring. (a) Displacement of the continuous GPS (CGPS) UTK1 receiver, showing the cumulative displacement along bearing 154∘ (the main direction of movement), from 14 November 2008 to 20 April 2015. Note all displacements are regionally filtered relative to the displacement of CGPS UTKU, which is located off the landslide. (b) Porewater pressures recorded above the slide plane in piezometers, PZA and UTK3. (c) Cumulative displacement of cGPS_UTK1 along bearing 154∘ and the daily porewater pressure recorded in piezometers, PZA, plotted in chronological order. (d) Displacement rate estimated along the horizontal bearing 154∘ for CGPS_porewater pressures recorded at piezometer PZA. All figures are taken and modified from Massey (2010) and Massey et al. (2013).
2.2 Earthquake-induced landslide displacement
No episodes of monitored landslide movement to date can be attributed to earthquake shaking. Earthquake ground accelerations were recorded during the observation period, of which the largest (ca. 1.0 m s−2) had a >20-year return period (Massey et al., 2016).
Massey (2010) and Massey et al. (2016) simulated the movement of the landslide under static conditions adopting (i) the lowest recorded piezometric head levels when the landslide was not accelerating; (ii) the mean maximum recorded piezometric head levels prior to the onset of the monitored periods of accelerated landslide movement, called “base levels”; and (iii) the mean maximum piezometric head levels recorded during the periods of accelerated landslide movement. They did this to calibrate the numerical models and adopted shear-strength parameters with the monitored movement and piezometric head levels recorded on the landslide. Using the calibrated models, and adopting the piezometric base levels, Massey et al. (2016) simulated the response of the landslide to 14 earthquakes, whose accelerograms span the range and type of earthquakes that could affect the site, with peak ground accelerations up to a 10 000-year return period (Stirling et al., 2012). The simulations adopted the decoupled method of Makdisi and Seed (1978), which is a modified version of the classic Newmark (1965) sliding block method that accounts for the dynamic response of the landslide mass as well as the permanent displacements accrued along the slide surface in response to the simulated earthquake. Massey et al. (2016) used the relationship between the yield acceleration (KY) and the maximum average acceleration of the landslide mass (Kmax) caused by an earthquake to determine the likely range of permanent displacements of the Utiku landslide in response to each of the 14 simulated earthquakes. KY was used to represent the critical yield acceleration, defined by Seed and Goodman (1964) as the minimum acceleration required to produce movement of the mass along a given slide surface. This effectively represents the increase in shear stress needed to reach the Mohr–Coulomb failure envelope of the slide surface material. Kmax was used to represent the peak average acceleration experienced by a given landslide mass along a given slide surface in response to the simulated earthquake. Simulated permanent landslide displacements were plotted against the ratio of . Thus, where , they represent a state where the shear stresses along the simulated slide surface exceed the Mohr–Coulomb failure envelope of the slide surface material and permanent displacement can occur, with larger displacements occurring at lower ratios. A ratio of 1.0 would indicate a state where any increase in shear stress would initiate movement, i.e. a safety factor of 1.0. The simulated landslide mass will not move at .
Annual frequencies of the peak ground accelerations (PGAs) from each of the 14 simulated accelerograms were estimated from the hazard curve for the site assuming Site Class B (Rock) (NZS1170) and adopting the New Zealand National Seismic Hazard Model (Stirling et al., 2012). Using the method of Moon et al. (2005), Massey et al. (2016) estimated that the mean annual permanent displacement of the landslide in response to the simulated earthquakes is 0.005–0.05 m yr−1 compared with historical and recent movement rates of the landslide (1972 to 2015), controlled by porewater pressure, that range from 0.04 to 0.07 m yr−1. The historical movement rates are similar to pre-historical rates (0.05–0.07 m yr−1) derived from radiocarbon dating and geomorphic indices. Thus, the results suggest that earthquake-induced displacements are not the primary driver of the long-term movement rate of the Utiku landslide.
3.1 Material sampling and physical properties
To obtain representative North Island Neogene mudstone samples, a 3 m deep trench was excavated into the active shear zone in the lower section of the Utiku landslide complex (Fig. 1a). To minimise sample disturbance and maintain field moisture conditions, block samples were hand dug from trench walls before being packaged and transported to the GNS laboratories for testing.
Physical property tests demonstrated that this material has a natural moisture content of 27.5 % with a liquid limit of 80 % and plastic limit of 37 %. The Atterberg limits indicate the mudstone is close to the boundary between very high plasticity silt and very high plasticity clay (defined in accordance with BS5930; BSI 1990).
3.2 Shear box experiments
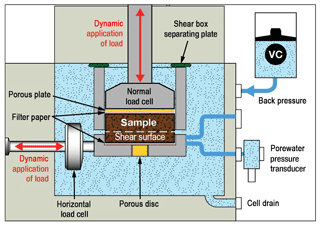
A suite of direct shear experiments was conducted in a dynamic back-pressured shear box (DBPSB). The DBPSB is a highly modified direct shear device, constructed by GDS Instruments Ltd and described in detail by Brain et al. (2015) and Carey et al. (2016, 2017). The apparatus can function as both a conventional direct shear and also a back-pressured shear machine and provides both static and dynamic control of horizontal (shear) and axial (normal) force and displacement, total stress, and effective stress. In addition, sample porewater pressure can be monitored throughout each experiment (Fig. 3).
Samples were fully saturated to simulate the shear zone conditions within the landslide complex during periods of movement using the methodology previously described by Carey et al. (2016). Consolidation was undertaken at effective stresses of 150 and 400 kPa by maintaining the total normal stress after saturation and reducing the back pressure. The normal load was applied through a feedback-controlled actuator that permitted the control of stress and sample displacement.
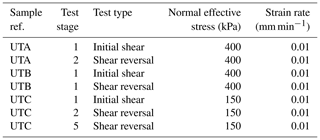
Following consolidation, three samples (UTA, UTB and UTC) were subject to an initial drained direct shear test (Table 1) to determine the Mohr–Coulomb strength envelope of the soil, and to generate a pre-existing shear surface for further testing. A slow displacement rate (0.001 mm min−1) was used to prevent the development of excess porewater pressures, and a full shear reversal was completed on each sample to ensure residual strength was achieved.
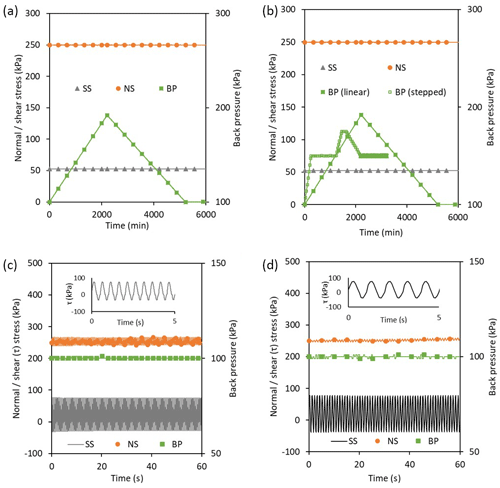
Figure 4Simulations of porewater pressure and earthquake-induced landslide movement mechanisms in the dynamic back-pressured shear box. (a) Linear increase and decrease in applied porewater pressure (back pressure, BP) at constant normal stress (NS) and shear stress (SS) from an initial mean effective stress of 400 kPa. (b) Linear (UTD PP1) and stepped (UTD PP2) increases and decreases in back-applied porewater pressure at constant normal stress and shear stress from an initial mean effective stress of 150 kPa. (c) Dynamic stress-controlled shear experiments conducted at a frequency of 2 Hz. (d) Dynamic stress-controlled shear experiments conducted at a frequency of 1 Hz.
A series of tests was undertaken under representative field stress paths (often termed pore pressure reinflation (PPR) tests; Petley et al., 2005) (Table 2). To replicate deep shear surface depths, an initial normal effective stress of 400 kPa was applied to sample UTB and 150 kPa was applied to sample UTC. These normal effective stresses were held constant whilst a shear stress of 75 % of residual shear strength at each normal effective stress (95 and 52 kPa) was applied, ramped at a rate of 1 kPa h−1 to avoid the generation of excess porewater pressures (Fig. 4a and b).
To explore the displacement response of the landslide shear surface to increasing and decreasing porewater pressures, samples UTB and UTC were subjected to different patterns of porewater pressure change at constant total normal and shear stresses (Fig. 4a and b). To measure the deformation response of the shear zone when pore pressures were increasing and decreasing, both samples were initially subjected to a linear increase in back pressures (applied porewater pressure) at a rate of 5 kPa h−1 to a pre-determined displacement limit of 6 mm, whereupon the back pressure was reduced at the same rate to the initial back pressure (100 kPa). To simulate more complex changes in the shear surface porewater pressure, a stepped pattern of back-pressure increases and decreases was applied to sample UTC over a similar time period. Between the linear PPR and stepped PPR tests for sample UTC, the conventional shear strength was measured during the shear reversal in order to determine whether any shear stress reduction occurred during the test stage (Table 1).
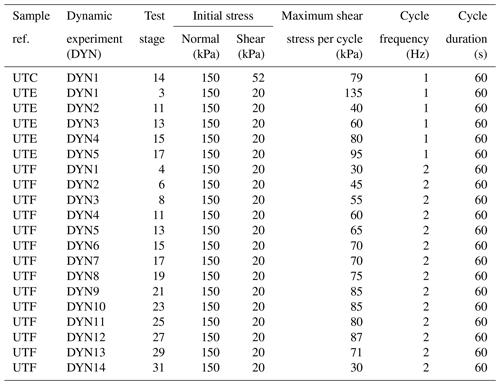
To simulate different amplitudes of earthquake shaking, we undertook a suite of dynamic shear experiments using samples UTC, E and F (Table 3). Each sample was tested with an initial normal effective stress of 150 kPa and an initial shear stress of 20 kPa, representing a stable slope condition. Following the initial shear stage, each sample was subjected to a series of dynamic shear-stress-controlled experiments at constant normal stress and back pressure (Fig. 4c and d). During each dynamic experiment a different maximum shear stress was applied to the sample and the horizontal (shear) displacement and porewater pressure response of the sample were measured (see Sect. 4).
A single dynamic shear experiment was undertaken on sample UTC (Table 3), at a frequency of 1 Hz for a duration of 60 s (i.e. 60 cycles in total), to assess the behaviour of a landslide shear surface previously subjected to rainfall-induced failure (Table 2). To assess the behaviour of a landslide shear surface during a large earthquake event and subsequent aftershocks (Table 3), sample UTE was subjected to a large initial dynamic shear experiment (DYN1) at 1 Hz for a duration of 60 s (60 cycles per test). The shear box was then reversed and the initial stress conditions were reapplied to the sample before four further dynamic shear stress experiments were carried out at the same frequency (Table 3). Fourteen further dynamic shear experiments were undertaken on sample UTF at a frequency of 2 Hz (120 cycles per test) to characterise progressive landslide behaviour during multiple dynamic events (Table 3).
To compare the results from the laboratory experiments with the simulated landslide displacements from Massey et al. (2016), we converted the permanent displacements from the laboratory measurements and numerical simulations into strain, and the static and dynamic shear stress acting on the mass of the laboratory sample, and simulated slide surface into acceleration. For each experiment we (1) calculated the mass of the sample under the applied static normal stress, which remained constant for all tests; (2) calculated the permanent displacement of the sample accrued during a single load cycle, during each test; (3) derived the yield acceleration of the sample from the initial stress state of each test, from the force (shear stress) needed to be applied to the sample to reach the conventional failure envelope; and (4) derived the maximum acceleration applied to the sample from the maximum force (shear stress) applied during each test per cycle, which we assume to be equivalent to Kmax. Although the force (shear stress) applied to each sample varied during a loading cycle, the maximum force (shear stress) applied during each cycle was set so that the given maximum value could not be exceeded.
4.1 Drained shear behaviour
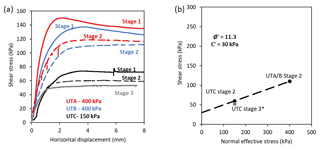
The drained shear experiments demonstrate a clear reduction in shear stress during each initial shear stage, which indicates progressive softening of the clay to residual state (Fig. 5a). The final shear stress at the end of each initial shear stage was used to calculate a residual Mohr–Coulomb strength envelope (ϕ=11.3∘, c=30 kPa; Fig. 5b). The residual strength parameters calculated from ring shear experiments on shear zone samples in the landslide (Kilsby, 2007) indicate ϕ=8.5∘ and c=4–10 kPa. Given that ring shear experiments typically produce parameters slightly lower than those determined from shear box experiments (Skempton, 1985), we infer our results to be broadly consistent with these previous measurements, although the difference in cohesion is notable. However, the ring shear experiments used samples that had been completely remoulded, whereas the shear box samples were intact. In addition, many clay-rich materials have been shown to have curved residual failure envelopes at low effective normal stresses (e.g. Lupini et al., 1981). We therefore deem this to have a negligible impact on our experiments and higher normal effective stresses.
4.2 Deformation response to changes in porewater pressure
In experiments UTB PP1 and UTC PP1 displacement initiated at a critical normal effective stress or porewater pressure threshold (Fig. 6a and b) as back pressure increased linearly. In both samples further increases in back pressure generated a rapid increase in displacement rate (Fig. 6a and b). During this phase of movement, the rate of porewater pressure increase lagged the applied back pressure, indicating that the porosity of the shear surface zone increased as the sample dilated. In both experiments we observed similar peak displacement rates (0.007 mm min−1), which were reached while porewater pressures were still increasing. Thereafter, the two samples demonstrated different displacement patterns. Sample UTB PP1 showed a decreasing trend in displacement rate before the peak porewater pressure was reached (Fig. 6c) whilst UTC PP1 showed a fluctuating, but near constant, displacement rate before peak porewater pressure was reached (Fig. 6d). In both experiments a reduction in the rate of increase in porewater pressure was observed as the shear surface mobilised, indicating that the shear zone dilated as the sample sheared, resulting in local dissipation of porewater pressures within the thin shear band.
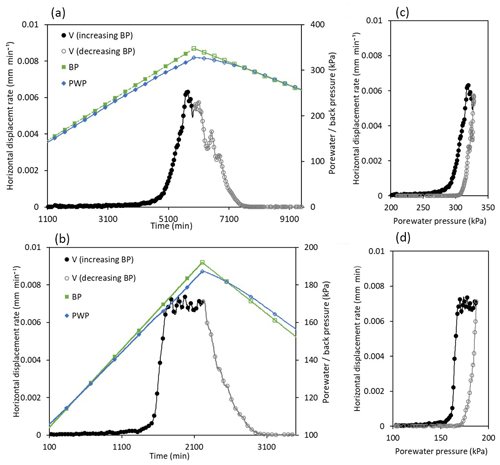
Figure 6Relationship between shear surface displacement rate (V) and porewater pressure (PWP) during linear pore pressure reinflation experiments conducted at mean effective stresses of 400 kPa (UTB PP1) and 150 kPa (UTC PP1). (a) Horizontal displacement rate against time in relation to the applied back pressure (BP) and measured porewater pressure (PWP, experiment UTC PP1). (b) Horizontal displacement rate against time in relation to the applied back pressure (BP) and measured porewater pressure (PWP, experiment UTB PP1). (c) Displacement rate against porewater pressure, experiment UTB PP1. (d) Displacement rate against porewater pressure, experiment UTC PP1.

Figure 7Relationship between shear surface displacement rate (V) and porewater pressure (PWP) during stepped pore pressure reinflation (BP) experiment conducted at mean effective stresses of 150 kPa (UTC PP2) for periods of increasing back pressure (solid symbols), constant back pressure (hollow symbols) and decreasing back pressure. (a) Horizontal displacement rate against time in relation to the applied back pressure (BP) and measured porewater pressure (PWP) experiment UTC PP2. (b) Horizontal displacement rate against porewater pressure experiment UTC PP2.
A complex relationship between shear surface displacement rate and porewater pressure was explored with a stepped PPR experiment (UTC PP2; Fig. 7a). The rapid increase in back pressure during stage 1 (Fig. 7a) resulted in a lag in the porewater pressure response, which we infer to be associated with low sample permeability. The change in porewater pressure induced an initial rapid increase in displacement rate followed by a reduction in rate as porewater pressures equilibrated (Fig. 7a). Thus, the displacement rate showed a transient component associated with a change in the porewater pressure. As the stress state equilibrated, the transient displacement rate component declines.
A further stepped increase in porewater pressure (stage 3) induced an associated transient increase in displacement rate (Fig. 7a and b). The displacement rate rapidly declined, however, even whilst applied porewater pressure (back pressure) was held stable (Fig. 7a and b, stage 4) and measured porewater pressure continued to rise.
In stage 5 porewater pressure was ramped down; at this point the rate of displacement rapidly declined to zero (Fig. 7a and b). In stage 6 the porewater pressure was held constant at a value greater than that at the initiation of displacement in this experiment. No displacement was recorded in this stress state. This behaviour, in which movement initiated at a lower porewater pressure than was the case when movement ceased, was consistent in both the linear PPR and stepped PPR experiments. The resultant hysteretic relationship between porewater pressure and displacement rate (Figs. 6c, d and 7b) was also observed within the landslide complex during periods of accelerated displacement (Massey et al., 2013).
Implications for landslide movement
Our experiments demonstrate a complex relationship between porewater pressure and displacement rate. The controlling factor appears to be a function of both the instantaneous porewater pressure value (i.e. the mean effective stress at that time) at the landslide shear surface and the rate of change of porewater pressure (i.e. the rate of change of normal effective stress). Given that, by definition, a change in stress must result in strain, two components of shear strain can be defined: first the stress state component () and second a transient stress state component defined by the change in normal effective stress state (). This relationship can be expressed using Eq. (1):
where v is the displacement rate, is the normal effective stress applied to the sample caused by a change (increase) in porewater pressure and represents the rate of change in normal effective stress generated by increasing porewater pressure.
We present a conceptual model (Fig. 8) to illustrate how this relationship controls landslide displacement during periods of elevated porewater pressure. The model shows that as porewater pressure increases the landslide remains stable until the mean effective stress is reduced to a critical condition at which displacement can occur (Fig. 8, stage A1). Once this movement is initiated the landslide displacement rate is a function of both the mean effective stress (background displacement rate component) and the rate of change of porewater pressure (transient displacement rate component). During periods when porewater pressures are constant, the rate of displacement is defined simply by the effective stress state. However, in periods of transient porewater pressures the displacement rate will be a combination of this stress state plus that generated by the changing stress state (Fig. 8, stage A2). A further increase in porewater pressure (reduction in mean effective stress) generates both a new stress state and a transient motion resulting in higher landslide displacement rates (Fig. 8, stages B1 and C1). When the effective stress state stabilises (Fig. 8, stage B2 and C2), the displacement rate reduces to its non-transient value. As porewater pressures reduce (mean effective stress increases) the negative change in porewater pressure produces a negative transient strain rate and consequently landslide displacement rates rapidly decline (Fig. 8, stage D3) or even cease.
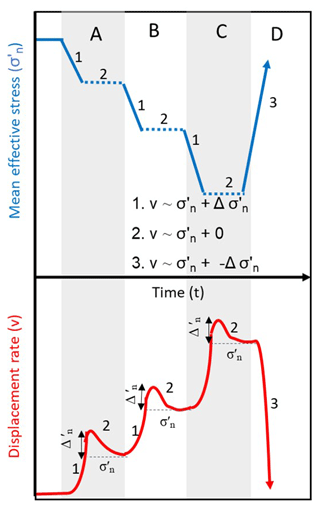
Figure 8Conceptual model of relationship between displacement rate and mean effective stress in a landslide in response to changes in porewater pressure.
The style of deformation described is consistent with ground movement responses measured within the Utiku landslide during periods of elevated porewater pressure (Massey et al., 2013). Movement rates clearly increased when the porewater pressure increased. However, movement rates rapidly declined when porewater pressures plateaued, and reduced to zero as soon as porewater pressures started to reduce. Thus, the behaviour is consistent in the field and the laboratory. Experiments on a silt from Lantau Island in Hong Kong showed similar behaviour (Ng and Petley, 2009; Petley et al., 2017). Furthermore, we speculate that this behaviour may also be consistent with the movement patterns observed in other slow-moving landslides, such as “stick–slip” behaviour (e.g. Allison and Brunsden, 1990).
4.3 Deformation during dynamic shear experiments
To characterise the displacement mechanisms in response to seismic excitation, we undertook a series of dynamic shear experiments at a constant normal effective stress of 150 kPa (chosen to be representative of the normal stress state in the landslide) on samples UTC, UTE and UTF (Fig. 9).
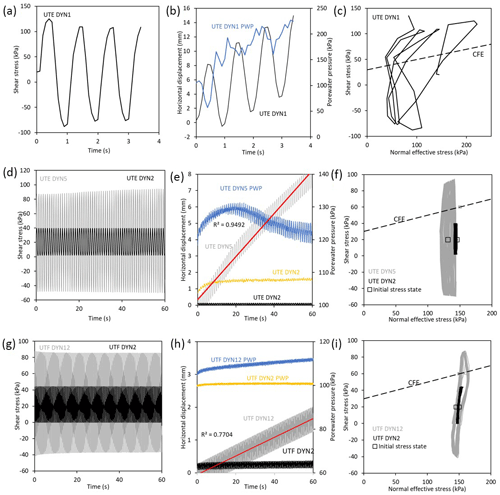
Figure 9Dynamic shear experiments. (a) Dynamic shear stress cycles applied at 1 Hz during experiment UTE DYN1. (b) Displacement and porewater pressure response measured during experiment UTE DYN1. (c) Sample stress paths in relation to the conventional failure envelope (CFE) during experiment UTE DYN1. (d) Dynamic shear stress cycles applied at 1 Hz in experiments UTE DYN2 and UTE DYN5. (e) Displacement and porewater pressure response measured during experiments UTE DYN2 and UTE DYN5. (f) Sample stress paths in relation to the conventional failure envelope (CFE) during experiments UTE DYN2 and UTE DYN5. (g) Dynamic shear stress cycles applied at 2 Hz during experiments UTF DYN2 and UTF DYN12. (h) Displacement and porewater pressure response measured during experiments UTF DYN2 and UTF DYN12. (i) Sample stress paths in relation to the conventional failure envelope (CFE) during experiments UTF DYN2 and UTF DYN12.
To evaluate how first-time failure may develop during seismic excitation, intact sample UTE was subject to a dynamic large-amplitude shear stress designed to significantly exceed the conventional failure envelope (Fig. 9a). A maximum shear stress of 120 kPa was reached during the first dynamic cycle (within 0.5 s), resulting in a displacement response of 8 mm over the same time period, indicating that the shear surface formed rapidly (Fig. 9b). This rapid displacement coincided with an initial increase in normal effective stress (Fig. 9c), which suggests that the sample dilated before subsequent cycles generated excess porewater pressure (Fig. 9b), reducing the normal effective stress significantly (Fig. 9c). Permanent displacement of the sample occurred at an approximately constant net rate per cycle until the experiment terminated within four cycles (3.5 s−1), the machine having reached its pre-set displacement limit (14 mm).
We observed that during experiments in which the applied maximum shear stress exceeded the conventional failure envelope, such as UTE DYN5 (Fig. 8d, e and f) and UTF DYN12 (Fig. 9g, h and i), and movement initiated and resulted in permanent displacement at a near-constant (possibly slightly declining) displacement rate per cycle (Fig. 9e and h). In each case we observed that displacement rates increased at higher shear stresses and generated higher excess porewater pressure (lower mean effective stresses) (Fig. 9b, e, h). Experiments in which shear stresses did not exceed the monotonic failure envelope, such as UTE DYN2 (Fig. 9f) and UTF DYN2 (Fig. 8i), displayed either no displacement or extremely low displacement rates, and there were negligible changes in porewater pressure (Fig. 9e and h, respectively).
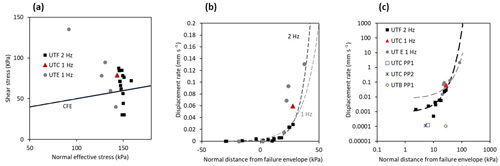
Figure 10Results of dynamic shear experiments undertaken at 1 and 2 Hz. (a) Average normal effective stress against maximum shear stress in relation to the conventional failure envelope (CFE). (b) Displacement rate against normal distance from the failure envelope. (c) Displacement rate against normal distance from the failure envelope in log scale including pore pressure experiments.
Using the method proposed by Brain et al. (2015), we use the average normal effective stress and the maximum shear stress (Fig. 10a) to plot displacement rates against the distance normal to the failure envelope during each experiment (Fig. 10b). This shows that dynamic stress changes that do not reach the conventional failure envelope generate negligible amounts of displacement. On the other hand, dynamic stress states that reach or exceed the failure envelope generate displacement rates that increase exponentially with distance normal to the conventional failure envelope (Fig. 10b). This relationship remains statistically valid for all samples tested, regardless of the initial stress state imposed, their stress history or frequency of seismic excitation applied. This demonstrates that the shear zone behaviour is controlled by a conventional Mohr–Coulomb relationship, indicating that the material strength characteristics remain constant and are not subject to strain hardening, weakening or rate effects. In Fig. 10c we have added the peak displacement rates for the PPR experiments using the same methodology. These experiments show that they generate significantly lower displacement rates than the trend for the dynamic tests. The later involve large, rapid changes in stress state (in this case shear stress), whereas the PPR experiments involve a much smaller rate of change in stress state. Thus, we would expect to have a much higher transient component to the displacement rate in the dynamic tests.
Implications for landslide movement
Our results suggest that permanent displacement of the Utiku landslide materials occurs when dynamic shear stresses exceed the conventional failure envelope of the sample and generate out-of-balance forces. The magnitude of displacement that occurs is a function of the magnitude and duration of the force imbalance. These results are consistent with previous studies, which consider more complex wave forms (Brain et al., 2015). We infer from our results that the frictional properties of the materials we tested do not increase (strain harden) or decrease (strain weaken) but remain constant during seismic excitation in the dynamic stress ranges examined. We anticipate, therefore, that the relationship between displacement rate and normal distance from the failure envelope would also be observed for complex seismic wave forms, but this requires further investigation.
To compare the small displacement observed in the laboratory and the large displacements of the entire landslide mass, we have calculated shear strain for different ratios derived from the dynamic laboratory experiments and the numerical simulations from Massey et al. (2016) (Fig. 11). Both datasets can be described by power law functions indicating that strain increases rapidly with decreasing ratios, showing that the tested material and the simulated landslide strains are both controlled by the amplitude of earthquake acceleration above the yield acceleration. The curves do not coincide perfectly as the lab and field tests started from a different stress state.
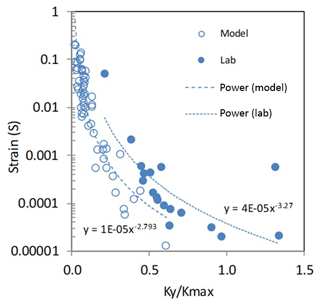
Figure 11Strain versus ratios from numerical simulations (hollow circles) and laboratory experiments (solid circles). Strain at given ratios of the yield acceleration (KY) to the maximum of the average acceleration of the mass (Kmax), in response to a given dynamic load adopting the piezometric base levels derived from field monitoring of piezometric head levels in the landslide.
Although very large accelerations cannot be simulated in the laboratory equipment, the power laws fitted to both datasets (Fig. 11) indicate that during strong earthquake accelerations strain will increase rapidly with relatively minor reductions in the ratio. From this we infer that the tested material and simulated landslide would undergo large strains (displacements) when accelerated by strong earthquakes.
These results show that dynamic changes in shear stress, which exceed the monotonic failure envelope of the shear surface material, result in permanent landslide displacement and movement rates several orders of magnitude greater than would be anticipated by similar magnitudes of normal effective stress reduction during periods of elevated porewater pressure. However, Massey et al. (2016) showed that the frequency of such large earthquake accelerations in the Utiku area is low, such that over the lifetime of the landslide most of the movements are associated with changes in porewater pressure. In an area with a higher occurrence of large-magnitude earthquakes, landslide behaviour would be more affected by coseismic displacements.
4.4 Understanding the movement of the Utiku landslide complex
Our data suggest that the clay seams controlling the movement of the Utiku landslide behave in a conventional manner, with no rate- or state-dependent friction characteristics. The landslide itself moves on a quasi-planar shear surface with comparatively low variation in thickness, rendering its behaviour comparatively simple. This makes it an ideal mass for which to explore response to porewater pressure and earthquake shaking.
In the experiments in which we explore the response to porewater pressure we find that the landslide starts to accumulate strain before the conventional residual Mohr–Coulomb failure envelope is reached (Fig. 7a, stage 1). We interpret this behaviour to be creep, in common with other studies (Petley et al., 2017). In this phase, the rate of movement is controlled by porewater pressure and there is a transient behaviour in response to changes in effective stress. This transient behaviour leads to a marked hysteresis in response to fluctuating porewater pressure, observable in both the laboratory experiment (Figs. 6b and 7b) and field monitoring (Fig. 2d) because the background strain rates are low.
Once the stress path reaches the failure envelope, the rate of movement is controlled by the out-of-balance forces. These experiments do not show classical critical state behaviour; instead, the stress path can exceed the failure envelope. In common with the results of Brain et al. (2015), we find that the rate of strain is determined by the normal distance from the failure envelope, which is a proxy for the magnitude of the out-of-balance force.
The same type of behaviour is seen in the dynamic tests. In this case, a strong correlation is seen between the maximum distance from the failure envelope in each cycle and the accumulated strain. Thus, the strain behaviour is controlled, and can be described, by understanding the stress path of the shear surface. The key modification is creep behaviour below the failure envelope, and the role of transient creep during periods of porewater pressure change.
Our alternative approach to examining the behaviour of the Utiku landslide invoked the analysis of Massey et al. (2016). In essence the yield acceleration can be considered to be the point at which the factor of safety reaches unity, whilst Kmax is the maximum acceleration – i.e. the maximum shear stress. Thus, the two approaches are describing the same stress state. Thus, the analysis also suggests that the static and dynamic behaviour of the Utiku landslide can be described using a conventional Mohr–Coulomb approach so long as the stress path is known.
In the case of Utiku, seismic accelerations can take the landslide into a state in which large strains can accumulate. However, in this case the frequency of such strong earthquakes occurring is low, such that little of the large accumulated displacement to date is likely to have originated from this mechanism. Displacements associated with elevated porewater pressures are much smaller but occur frequently. The laboratory tests corroborate the results of Massey et al. (2016), that the cumulative effect of porewater-pressure-induced displacements over the life of the landslide is large, such that the total displacement to date is likely to have been dominated by the effects of elevated porewater pressures.
In our study we have used a dynamic back-pressured shear box to simulate representative stress conditions in a slow-moving landslide in Neogene mudstones during phases of porewater pressure fluctuation and seismic excitation. The results provide new insight into their movement mechanisms.
-
During periods of elevated porewater pressure, displacement rates are influenced by two components: first an absolute effective stress state component (normal effective stress) and second a transient effective stress state component (the rate of change of normal effective stress). The behaviour observed in the laboratory is consistent with the ground monitoring records, confirming the previous findings of Massey et al. (2013), and helping to explain the differing relationships between displacement rate and porewater pressure during periods of acceleration and deceleration in some slow-moving landslides.
-
During dynamic shear we show that displacement rates are controlled by the extent to which the forces operating at the shear surface are out of balance. Once these forces exceed the yield acceleration, displacement rates increase rapidly with distance normal to the failure envelope in plots of shear stress against normal effective stress.
-
The laboratory results presented in this paper, when combined with the dynamic modelling results from Massey et al. (2016), indicate that during strong earthquake accelerations, strain will increase rapidly with relatively minor increases in the out-of-balance forces (reducing the ratio). Therefore, our laboratory results corroborate the findings of Massey et al. (2016), that large landslide displacements could occur when accelerated by strong earthquakes, but there is evidence that such accelerations in the study area do not occur frequently. Thus, in this area over long (i.e. multiple seismic cycle) timescales, landslide displacement is predominantly controlled by porewater pressures.
By combining the specialised laboratory testing with field monitoring, well-constrained ground models and numerical simulations, we have shown how the mechanisms of deformation occurring along a landslide shear surface control the movement patterns of many large slow-moving translational landslides. The development of such approaches provides a framework, which can be used in complex hazard assessment of landslides, that could be mobilised for both strong earthquakes and significant rain events.
The landslide monitoring data can be downloaded from https://www.geonet.org.nz/data/gnss/map (GeoNet, 2019). Laboratory experimental data can be provided by the authors on request.
JMC designed and undertook the laboratory experiments. CIM undertook the ground movement monitoring analysis and numerical modeling. BL supported throughout the laboratory experiments. DNP assisted in the experimental design and analysis. All authors contributed to writing the article.
The authors declare that they have no conflict of interest.
We thank GNS Science staff Stuart Read and Zane Bruce for laboratory support and Mauri McSaveney for his helpful discussions and suggestions throughout the study.
This research has been supported by the Earthquake Commission (grant no. 16/721), the GNS Science GeoNet project, the GNS Science Strategic Science Investment Fund and by the NERC/ESRC Increasing Resilience to Natural Hazards programme (grant NE/J01995X/1), and NERC/Newton Fund (grant NE/N000315).
This paper was edited by Xuanmei Fan and reviewed by Theo W. J. van Asch and one anonymous referee.
Allison, R. and Brunsden, D.: Some mudslide movement patterns, Earth Surf. Proc. Land., 15, 297–311, 1990.
Angeli, M. G., Gasparetto, P., Menotti, R. M., Pasuto, H., and Silvano, S.: A visco-plastic model for slope analysis applied to a mudslide in Cortina d'Ampezzo, Italy, Q. J. Eng. Geol. Hydroge., 29, 233–240, 1996.
Angeli, M. G., Gasparetto, P., and Bromhead, E.: Strength-regain Mechanisms in Intermittently Moving Landslides, Proceedings of the 9th International Symposium on Landslides, 28 June–2 July 2004, Rio de Janeiro, Brazil, 1, 689–696, 2004.
Bertini, T., Cugusi, F., D'Elia, B., and Rossi-Doria, M.: Climatic Conditions and Slow Movements of Colluvial Covers in Central Italy, Proceedings of the IV International Symposium on landslides, 16–21 September 1984, Toronto, Canada, 1, 367–376, 1984.
Brain, M. J., Rosser, N. J., Sutton, J., Snelling, K., Tunstall, N., and Petley, D. N.: The effects of normal and shear stress wave phasing on coseismic landslide displacement, J. Geophys. Res.-Earth, 120, 1009–1022, 2015.
British Standards Institute (BSI): British standard methods of test for soils for civil engineering purposes. Part 1: General requirements and sample preparation. BS 1377: Part 1. Board. US National Research Council, Washington, DC, USA, 36–75 Special Report 247, 1990.
Carey, J. M., McSaveney, M. J., Lyndsell, B. M., and Petley, D. N.: Laboratory simulation of a slow landslide mechanism, in: Landslides and engineered slopes: experience, theory and practice: proceedings of the 12th International Symposium on Landslides, 12–19 June 2016, Naples, Italy, edited by: Aversa, S., Cascini, L., Picarelli, L., and Scavia, C., 2, 557–564, 2016.
Carey, J. M., McSaveney, M. J., and Petley, D. N.: Dynamic liquefaction of shear zones in intact loess during simulated earthquake loading, Landslides, 14, 789–804, 2017.
Collins, B. D. and Jibson, R. W.: Assessment of existing and potential landslide hazards resulting from the April 25, 2015 Gorkha, Nepal earthquake sequence, U.S. Geological Survey Open-File Report 2015–1142, 50 pp., https://doi.org/10.3133/ofr20151142, 2015.
Corominas, J., Moya, J., Ledesma, A., Lloret, A., and Gili, J.A.: Monitoring of the Vallcebre landslide, Eastern Pyrenees, Spain, Proceedings of the International symposium on Slope Stability Engineering. IS-Shikoku' 99, 8–11 November 1999, Matsuyama, Japan, 1239–1244, 1999.
Corominas, J., Moya, J., Ledesma, A., Lloret, A., and Gill, J. A.: Prediction of Ground Displacements and Velocities from Groundwater Level Changes at the Vallebre Landslide (Eastern Pyrenees, Spain), Landslides, 2, 83–96, 2005.
Dellow, G. D., McSaveney, M. J., Stirling, M. W., and Berryman, K. R.: A Probabilistic Landslide Hazard Model for New Zealand, in: Geological Society of New Zealand 50th Annual Conference, 28 November–1 December 2005, Kaikoura, New Zealand, Programme & Abstracts, edited by: Pettinga, J. R. and Wandres, A. M., 119A, Geological Society of New Zealand Miscellaneous Publication, p. 24, 2005.
Dreyfus, D., Rathje, E. M., and Jibson, R. W.: The influence of different simplified sliding-block models and input parameters on regional predictions of seismic landslides triggered by the Northridge earthquake, Eng. Geol., 163, 41–54, 2013.
Froude, M. J. and Petley, D. N.: Global fatal landslide occurrence from 2004 to 2016, Nat. Hazards Earth Syst. Sci., 18, 2161–2181, https://doi.org/10.5194/nhess-18-2161-2018, 2018.
GeoNet: Geological hazard information for New Zealand, available at: https://www.geonet.org.nz/data/gnss/map, last access: 5 August 2019.
Gonzalez, D. A., Ledesma, A., and Corominas, J.: The viscous component in slow-moving landslides: a practical case, in: Landslides and Engineered Slopes, Proceedings of the 10th International Symposium on Landsldies and Engineered Slopes, 30 June–4 July 2018, Xian, China, edited by: Chen, Z., Zhang, J.-M., Ho, K., Wu, F.-Q., and Li, Z.-K., 237–242, 2008.
Hovius, N., Meunier, P., Lin, C.-W., Chen, H., Chen, Y.-G., Dadson, S., Horng, M.-J., and Lines, M.: Prolonged seismically induced erosion and the mass balance of a large earthquake, Earth Planet. Sci-. Lett., 304, 347–355, 2011.
Hungr, O., Leroueil, S., and Picarelli, L.: The Varnes classification of landslide types, an update, Landslides, 11, 167–194, 2014.
Jibson, R. W.: Methods for assessing the stability of slopes during earthquakes – A retrospective, Eng. Geol., 122, 43–50, 2011.
Keefer, D. K.: The importance of earthquake-induced landslides to long-term slope eroion and slope-failure hazards in seismically active regions, Geomorphology, 10, 265–284, 1994.
Kilsby, C.: An engineering geological appraisal of the Utiku Landslide, North Island, New Zealand, MSc Thesis, University of Portsmouth, Portsmouth, UK, 2007.
Lee, E. M., Bland, K. J., Townsend, D. B., and Kamp, P. J. J.: Geology of the Hawkes Bay area. 1 : 25 000 geological map 8, Institute of Geological and Nuclear Sciences Limited, Lower Hutt, New Zealand, 2012.
Leroueil, S., Locat, J., Vaunat, J., Picarelli, L., and Faure. R.: Geotechnical characterisation of slope movements, in: Proceedings of the Seventh International Symposium on Landslides, 17–21 June 1996, edited by: Senneset, K., Trondheim, Norway, Balkema, Rotterdam, the Netherlands, 1, 53–74, 1996.
Li, G., West, A. J., Densmore, A. L., Jin, Z., Parker, R. N., and Hilton, R. G.: Seismic mountain building: Landslides associated with the 2008 Wenchuan earthquake in the context of a generalized model for earthquake volume balance, Geochem. Geophy. Geosy., 15, 833–844, 2014.
Lupini, J. F., Skinner A. E., and Vaughan P. R.: The drained residual strength of cohesive soils, Geotechnique, 31, 181–213, 1981.
Makdisi, F. I. and Seed, H. B.: Simplified procedure for evaluating embankment response, J. Geotech. Eng.-ASCE, 105, 1427–1434, 1978.
Massey, C. I.: The dynamics of reactivated landslides: Utiku and Taihape, North Island, New Zealand, PhD thesis, Durham University, Durham, UK, 2010.
Massey, C. I., Petley, D. N., and McSaveney, M. J.: Patterns of movement in reactivated landslides, Eng. Geol., 159, 1–19, 2013.
Massey, C. I., Abbott, E. R., McSaveney, M. J., Petley, D. N., and Richards, L.: Earthquake-induced displacement is insignificant in the reactivated Utiku landslide, New Zealand, in: Landslides and engineered slopes: experience, theory and practice: proceedings of the 12th International Symposium on Landslides, 12–19 June 2016, edited by: Aversa, S., Cascini, L., Picarelli, L., and Scavia, C., Boca Raton, Fla., USA, 31–52, 2016.
Massey, C. I., Townsend, D. B., Rathje, E., Allstadt, K. E., Lukovic, B., Kaneko, Y., Bradley, B., Wartman, J., Jibson, R. W., Petley, D. N., Horspool, N. A., Hamling, I. J., Carey, J. M., Cox, S. C., Davidson, J., Dellow, G. D., Godt, G. W., Holden, C., Jones, K. E., Kaiser, A. E., Little, M., Lyndsell, B. M., McColl, S., Morgenstern, R. M., Rengers, F. K., Rhoades, D. A., Rosser, B. J., Strong, D. T., Singeisen, C., and Villeneuve, M.: Landslides triggered by the 14 November 2016 Mw 7.8 Kaikoura earthquake, New Zealand, B. Seismol. Soc. Am., 108, 1630–1648, https://doi.org/10.1785/0120170305, 2018.
Mcoll, S. T. and McCabe, M.: The causes and Agricultural impacts of large translational landslides: Case studies from North Island, New Zealand, in: Landslides and engineered slopes: experience, theory and practice: proceedings of the 12th International Symposium on Landslides, 12–19 June 2016, edited by: Aversa, S., Cascini, L., Picarelli, L., and Scavia, C., Boca Raton, Fla., 1401–1408, 2016.
Moon, A. T., Wilson, R. A., and Flentje, P.: Developing and using landslide size frequency models, in: Proceedings of the International Conference on Landslide Risk Management, 18th Annual Vancouver Geotechnical Society Symposium, Vancouver, Canada, 31 May–4 June 2005, 589–598, available at: http://ro.uow.edu.au/engpapers/384 (last access: 2 August 2019), 2005.
Newmark, N.: Effects of earthquakes on dams and embankments, Geotechnique, 15, 139–160, 1965.
Ng, K.-Y. and Petley, D. N.: A process approach towards landslide risk management in Hong Kong, Q. J. Eng. Geol. Hydroge., 42, 487–498, 2009.
Petley, D. N.: Global patterns of loss of life from landslides, Geology, 40, 927–930, 2012.
Petley, D. N., Higuchi, T., Bulmer, M. H., and Carey, J.: The development of progressive landslide failure in cohesive materials, Geology, 30, 719–722, 2005.
Petley, D. N., Dunning, S. A., Rosser, N. J., and Kausar, A. B.: Incipient landslides in the Jhelum Valley, Pakistan following the 8th October 2005 earthquake, in: In Disaster Mitigation of Debris Flows, Slope Failures and Landslides, edited by: Marui, H., Universal Academy Press, Tokyo, Japan, 47–56, 2006.
Petley, D. N., Carey, J. M., Ng, K.-Y., Massey, C. I., and Froude, M. J.: Understanding patterns of movement for slow moving landslides, in: 20th Symposium of the New Zealand Geotechnical Society, 24–26 November 2017, edited by: Alexander, G. J. and Chin, C. Y., Napier, New Zealand, 2017.
Picarelli, L.: Considerations about the mechanics of slow active landslides in clay, chap. 3, in: Progress in Landslide Science, edited by: Sassa, K., Fukuoka, H., Wang, F., and Wang, G., Springer-Verlag, Berlin, Hiedelberg, Germany, 27–57, 2007.
Rosser, B. J., Dellow, G. D., Haubrock, S. N., and Glassey, P. J.: New Zealand's National Landslide Database, Landslides, 14, 1949–1959, 2017.
Seed, H. B. and Goodman, R. E.: Earthquake stability of slopes of cohesionless soils, Journal of the Soil Mechanics and Foundations Division, 90, 43–74, 1964.
Skempton, A. W.: Residual Strength of Clays in Landslide, Folded Strata and the Laboratory, Geotechnique, 35, 3–18, 1985.
Stirling, M., McVerry, G., Gerstenberger, M., Litchfield, N., Van Dissen, R., Berryman, K., Barnes, P., Wallace, L., Bradley, B., Villamor, P., Langridge, R., Lamarche, G., Nodder, S., Reyners, M., Rhoades, D., Smith, W., Nicol, A., Pettinga, J., Clark, K., and Jacobs, K.: National Seismic Hazard Model for New Zealand: 2010 Update, B. Seismol. Soc. Am., 102, 1514–1542, 2012.
Stout, M. L.: The Utiku landslide, North Island, New Zealand, Geological Society of America: Reviews in Engineering Geology, 3, 171–184, 1977.
Thompson, R. C.: Relationship of geology to slope failures in soft rocks of the Taihape-Mangweka area, Central North Island, New Zealand, PhD Thesis, University of Auckland, Auckland, New Zealand, 1982.
Valagussa, A., Frattini, P., Crosta, G. B., and Valbuzzi, E.: Pre and post Nepal earthquake landslide inventories, in: Landslides and engineered slopes: experience, theory and practice: proceedings of the 12th International Symposium on Landslides, 12–19 June 2016, edited by: Aversa, S., Cascini, L., Picarelli, L., and Scavia, C., Boca Raton, Fla., USA, 1957–1964, 2016.
van Asch, W. J., Malet, J. P., and Bogaard, T. A.: Problems in predicting the mobility of slow-moving landslides, Eng. Geol., 91, 45–55, 2007.
Wilson, R. C. and Keefer, D. K.: Dynamic analysis of a slope failure from the 6 August 1979 Coyote Lake, California, earthquake, B. Seismol. Soc. Am., 73, 863–877, 1983.