2.1 Identifying river deltas

River deltas are fundamentally systems of sediment accumulation and distribution at the coastline. Accordingly, we identify coastal deltas by distinguishing geomorphic expressions of sediment accumulation and distribution at locations where rivers meet the coast. We consider a river to have formed a delta at the coastline if the river-mouth area contains an active or relict distributary network (Fig. 1e), ends in a subaerial depositional protrusion from the lateral shoreline (Fig. 1d), or does both (Fig. 1c). Distributary networks are an expression of sediment deposition and distribution (Edmonds et al., 2011) and we identify them by the presence of one or more channels that bifurcate and intersect the coast at different locations. We include relict channels, where they are clearly visible in imagery and connect to the main channel, because they are evidence of sediment distribution and accumulation through avulsion (Slingerland and Smith, 2004). We do not include channels that bifurcate solely around non-deltaic topographic highs. Our second criterion is oceanward-directed shoreline protrusions. We classify a protrusion as deltaic if it has a relatively smooth depositional shoreline, as opposed to rough shorelines associated with rocky coasts (Limber et al., 2014), and if it extends more than approximately five channel widths oceanward relative to the position of the regional shoreline. We map only protrusions that are associated with the river, ignoring protrusions that may exist near the channel mouth that we judge to be preexisting undulations in the shoreline. Examples of this include promontories associated with preexisting geology or depositional protrusions created by other processes, such as wave-driven sediment transport (Ashton et al., 2001). Our delta identification method does not account for deltaic deposition with no geomorphic signature, such as a single-channel delta infilling a drowned valley that produces no protrusion from the regional shoreline. Although such features may be considered deltaic, we cannot unambiguously identify them as deltas based on aerial imagery alone and we do not include them in the dataset.

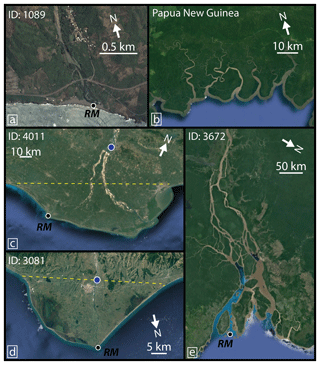
Figure 1Examples of (a) a river mouth without a delta (Mexico), (b) headless tidal channels not included in this dataset, (c) a delta with land both upstream and downstream of the regional shoreline vector (marked by dashed line – location of delta node demarcated with blue dot; Godavari River, India), (d) a delta distinguished by a shoreline protrusion only (Red River, Turkey), and (e) a delta distinguished by a distributary channel network only. RM locations mark the main river channel mouth (Amazon River, South America). Map data: ©Google and DigitalGlobe.

We applied the preceding criteria to a scan of marine coastlines, including most open-ocean coasts and the Black Sea, using Google Earth. First, we identified all rivers with width >50 m reaching the coast that are connected to an upstream catchment (Fig. 1a, c–e). Channels not clearly connected to an upstream catchment, such as tidal channels, were not included in the dataset (Fig. 1b). This was done to restrict the study to coastal depositional landforms that represent the interaction of upstream and downstream environmental variables. We selected rivers at least 50 m in width because they have corresponding data, such as basin area, that can be reliably determined on coarser-resolution elevation models. This width designation was applied to the river bankfull widths and thus includes any visible mid-channel bars. Channel widths on rivers without a delta were measured at the shoreline or upstream from visible marine influence, such as significant tidal widening (Nienhuis et al., 2018). If a river empties into a gradually widening estuary or embayment, we measured the channel width where it is devoid of a significant downstream widening and thus representative of the river. Channel widths on rivers that have deltas were measured immediately upstream of the delta node, which we define as the location of the most upstream bifurcation. If no bifurcation exists, we use the intersection of the main channel with the regional shoreline (e.g., Fig. 1c and d, blue dot). In all cases, channel widths were not measured in areas of clear human influence. This includes, for example, man-made levees that can cause artificial widening or narrowing of channels.

We mapped rivers and deltas on the coastlines of Earth's continents and large islands (Fig. 2). We exclude small islands where rivers large enough for inclusion are rare and it is difficult to obtain environmental data. Thus, large islands, such as Papua New Guinea and Fiji, were included but not all the associated smaller islands. Coastlines dominated by fjords (as determined using Dürr et al., 2011) were not included because offshore glacial over-deepening and protection from coastal waves and tides make their comparison to most of the world's coastal deltas difficult. Ephemeral rivers in arid regions were included in the dataset, though the rivers in these regions are often difficult to identify due to poor imagery and difficulty distinguishing the channel banks when they are dry. If a clear distinction was not possible, the river was not included in the dataset. Thus, the total count of rivers and deltas in arid regions should be considered a minimum. Finally, we did not include river channels that do not clearly reach the coast to avoid conflating alluvial fans with deltas.

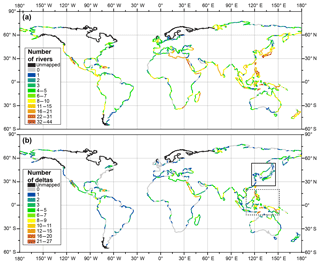
Figure 2Global distribution of coastal (a) rivers (includes both river mouths and deltas) and (b) deltas only. Each colored line segment is 3^∘ long. Black (solid and dashed) boxes refer to hotspots of delta formation discussed in the text.

For each river we marked the latitude and longitude of the main river mouth (Fig. 1, RM) (Table S1 in the Supplement). For rivers without a delta, this is the location where the river meets the coastline (Fig. 1a), and for rivers with deltas, this is the location of the widest river mouth in the distributary network (Fig. 1c–e). For rivers sheltered by barrier islands or rocky islands, we mark the river mouth landward of those obstructions.

2.2 Environmental variables

To determine controls on delta formation we also compiled data on eight environmental variables (Table 1). We classify the environmental variables into two groups: (1) upstream variables include water and sediment supply from the river, sediment concentration, and the drainage basin area; (2) downstream variables include wave height, tidal range, bathymetric slope immediately offshore of the river mouth, and the rate of sea level change. We use modern data collected for each of these environmental variables, even though some deltas may have initially formed under different conditions 6000 to 8500 years ago as sea level rise slowed after deglaciation (Stanley and Warne, 1994). We assume that the current river delta (or lack thereof) is adapted to the modern environmental variables because scaling analyses suggest that the diffusive response time of river delta deposition and wave reworking is on the order of 100–1000 years (Jerolmack, 2009; Nienhuis et al., 2013). Of course, the diffusive response time depends nonlinearly on delta size, so larger deltas may still be adapting to changing environmental variables.

Notably absent in the collected environmental variables are tectonic data. At present, there are no globally available measurements of tectonic activity (e.g., uplift). However, we consider some of the variables to be reasonable proxies for tectonics. For instance, models predicting sediment flux to the ocean represent tectonics in the form of basin area (Syvitski and Morehead, 1999; Syvitski and Milliman, 2007). We also include bathymetric slope, which is a rough proxy for tectonics, because on average tectonically active margins have steeper slopes than passive margins (Pratson et al., 2007).

Table 1Independent variables: upstream and downstream environmental variables.

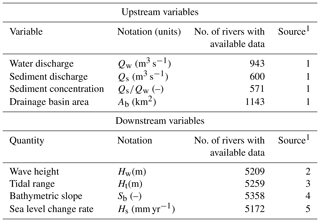
¹ Sources: 1. Milliman and Farnsworth (2011), 2. WAVEWATCH, 3. OSU TOPEX/Poseidon Global Inverse Solution TPXO, 4. ETOPO1, 5. AVISO (https://www.aviso.altimetry.fr, last access: 11 August 2018).

Download Print Version | Download XLSX

3.1 Global distribution of rivers and deltas

River deltas are not distributed evenly on coastlines and there are locations on the world's coastlines where deltas are unusually common (Fig. 2). These “delta hotspots” occur primarily in Southeast Asia (dashed box Fig. 2b). Notably, these areas are also densely populated with rivers (Fig. 2a), though river abundance does not always equate to delta abundance. For example, East Asia has a high river density but low delta density (black box, Fig. 2b). Similarly, along the west coasts of central and southern North America (from 5 to 45^∘ N) the coast is densely populated with rivers, but the northern portion is delta-poor compared to the southern portion. There are also a surprising number of deltas in arid environments. For instance, there is high delta density in the Red Sea and on Baja California. This largely arises because many alluvial fans coming off the nearby mountains reach the coastline and satisfy our definition of a delta.

Binning these data by latitude reveals preferential locations of rivers and deltas (Fig. 3). The largest numbers of rivers and deltas occur roughly from −12 to 45^∘ and 66 to 72^∘ (Fig. 3a). This unequal distribution is partly explained by the unequal latitudinal distribution of global shoreline length (Wessel and Smith, 1996) (Fig. 3b). River density, or rivers per shoreline kilometer, shows that globally there is one river for every 230 km of coastline and one delta for every 333 km of coastline. Coastlines within the −6 to −3^∘ bin have the highest density of deltas with roughly one delta per 100 km of shoreline (Fig. 3c, solid black line). River density is above average from −45 to 45^∘ (Fig. 3c, white bars). Delta density, however, is above average over a smaller range from −21 to 30^∘ (Fig. 3c, solid black line).

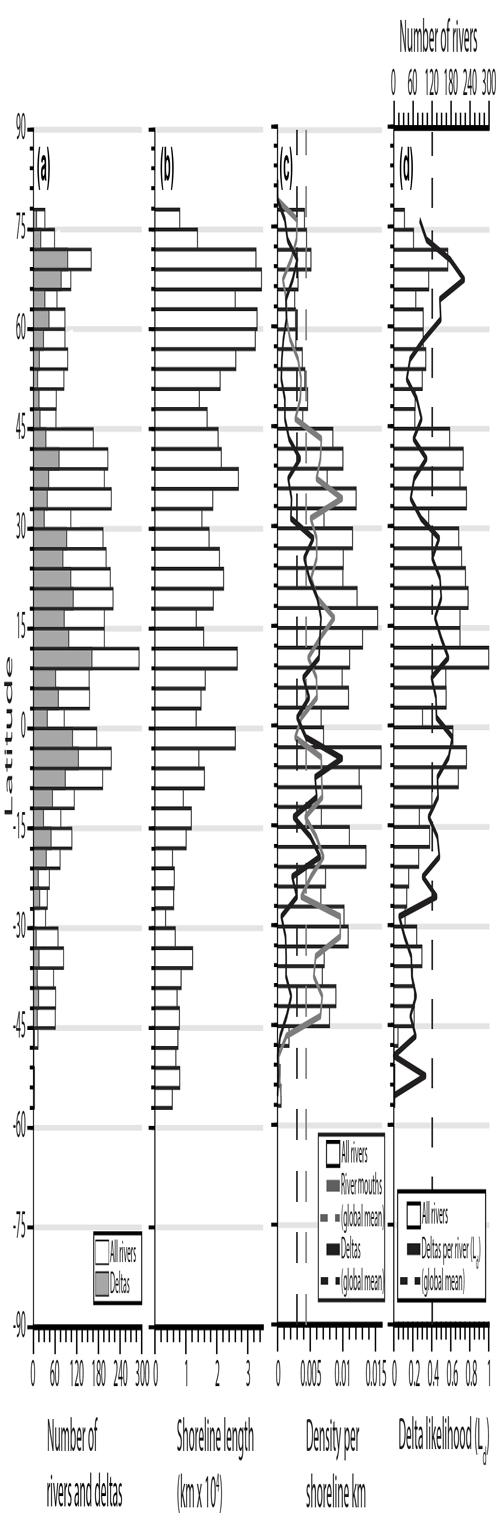
Figure 3Histograms showing the latitudinal distribution (3^∘ bins) of (a) the total number of rivers (white) and number of rivers with deltas (gray), (b) the total shoreline length of surveyed coastlines measured from the global shoreline database (Wessel and Smith, 1996), and (c) all rivers (including deltas) per shoreline kilometer (white bars), for which the solid gray line shows rivers with no deltas (river mouths) and the solid black line shows rivers with deltas. (d) The solid black line is the ratio of deltas per river (delta likelihood, L_d), and the white bars are the total number of rivers (including deltas).

Download

To determine which environments promote delta formation, it is perhaps most instructive to observe locations where the likelihood for rivers to create deltas is highest. Delta likelihood (L_d) is defined as the number of deltas relative to the total number of rivers for a given set of samples (Fig. 3d, solid black line). For the entire dataset, 40 % of rivers form deltas, and thus the global L_d is 0.40 (Fig. 3d, dashed black line). Regions where L_d is higher than the global mean are from −27 to 30^∘ and 60 to 72^∘, whereas rivers located from −57 to −27^∘ and 30 to 60^∘ are least likely to form a delta (Fig. 3d).

These latitudinal zones, where rivers are more likely to create deltas, coincide with peaks in environmental variables that influence delta formation. Both Q_w and Q_s have peaks from roughly −9 to 30^∘ and 60 to 75^∘ (Fig. 4a, b), which are similar in location to L_d peaks. A_b has a similar high-latitude peak but is missing the equatorial peak (Fig. 4d), probably reflecting the importance of small mountainous rivers in those locations (Milliman and Syvitski, 1992). On the other hand, delta formation is infrequent where H_w and H_t are high, namely −57 to −27^∘ and 42 to 60^∘ (Fig. 4e, f). There are no latitudinal changes in Q_s∕Q_w, S_b, or H_s that are easily relatable to delta formation (Fig. 4c, g, h).

Figure 4Latitudinal variation of the independent variables used in this study. All panels show the median value for 3^∘ bins: (a) water discharge, Q_w; (b) sediment discharge, Q_s; (c) sediment concentration, Q_s∕Q_w; (d) drainage basin area, A_b; (e) mean annual significant wave height, H_w; (f) median tidal range, H_t; (g) bathymetric slope, S_b; (h) rate of sea level change, H_s. For (a, c, d) the outliers have been cut off for viewing purposes.

Download

3.2 Relationships between environmental variables and delta formation

We explore controls on delta formation by analyzing how the likelihood of a river creating a delta varies with each environmental variable. River mouths and deltas have statistically different population distributions for seven of the eight environmental variables (all but Q_s∕Q_w) (Table 2), suggesting that deltas form under certain ranges of environmental variables. To determine this, we used the Kolmogorov–Smirnov test, which is a nonparametric, distribution-free test that uses the cumulative distribution functions of the two populations to estimate statistical difference. Although a few variable pairs show some correlation, such as Q_w and A_b, none have a strong statistical correlation (Pearson correlation coefficient >0.9), suggesting they exert largely independent controls on delta formation.

Table 2Statistical differences between rivers with no deltas and rivers with deltas. Percentages are calculated relative to the total number of rivers with no deltas (3225) and with deltas (2174). D is the two-sample Kolmogorov–Smirnov test statistic and is equal to the maximum variance between the cumulative distribution functions of the two populations tested; p is the p value at the 5 % significance level, and h is the test decision, wherein 1 rejects the null hypothesis that the distributions are from the same population and 0 accepts the null hypothesis.

Download Print Version | Download XLSX

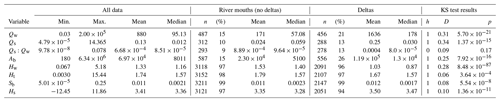
Delta likelihood (L_d) generally increases as the upstream environmental variables increase (Fig. 5). Increasing Q_w, Q_s, and A_b causes a linear increase in semi-log space in L_d (Fig. 5a, b, d). Deltas have characteristic Q_w, Q_s, and A_b values that are an order of magnitude larger than those of river mouths (statistically significant, p<0.05) (Table 2). These data suggest that rivers with small water and sediment discharge and/or that come from small drainage basins rarely form deltas, whereas rivers with larger values of the upstream variables frequently create deltas. Sediment concentration (Q_s∕Q_w) exerts no clear control on L_d (Fig. 5c), and there is no statistical difference between the mean or median Q_s∕Q_w values for river mouths versus those for deltas (Table 2).

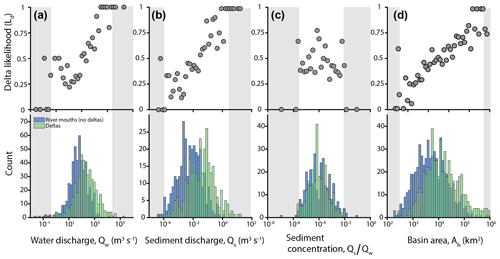
Figure 5Differences in upstream environmental variables for rivers with and without deltas. Scatter plots (top of each panel) of delta likelihood, defined as the number of rivers with a delta relative to the total number of rivers in that interval. Histograms (bottom of each panel) binned into equal log-spaced intervals. Gray boxes outline ranges represented by 1 % or less of the total sample number.

Download

Rivers are less likely to create deltas where H_w and H_t are large. L_d shows a clear linear decrease as H_w increases (Fig. 6a). Rivers that experience little wave energy at the coast (H_w<1 m) create a delta more than half of the time (L_d≈0.5–0.6), but delta formation becomes nearly impossible for larger wave heights. L_d also seems to show a linear decrease with H_t (Fig. 6b) if the long tail of the distribution is eliminated where the sample size is small (H_t>7 m). The population of river mouths has higher mean and median H_w and H_t than rivers with deltas (statistically significant, p value <0.05) (Table 2).

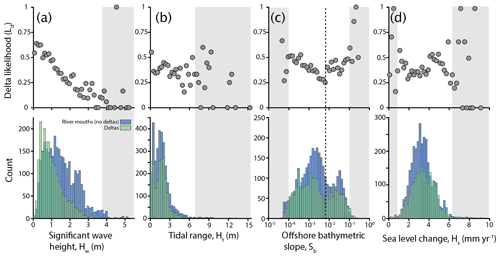
Figure 6Differences in downstream environmental variables for rivers with and without deltas. Scatter plots (top of each panel) of delta likelihood, defined as the number of rivers with a delta relative to the total number of rivers in that interval. Histograms (bottom of each panel) binned into equal log-spaced intervals. Gray boxes outline ranges represented by 1 % or less of the total sample number. Sea level change plot and histogram (d) only include positive values due to limited negative values.

Download

S_b displays a non-monotonic relationship in which L_d decreases then increases across the range (Fig. 6c). S_b data are bimodally distributed for the rivers in our dataset, suggesting rivers empty into two types of receiving basins (separated by the dashed line in Fig. 6c). If these basin types are separated, there is a clearer relationship between S_b and L_d. For shallowly dipping basins (S_b<0.006), there is a negative relationship between L_d and S_b (Fig. 6c, left of dashed line), and delta likelihood increases as slope decreases. In steeply dipping basins (S_b>0.006), L_d is approximately constant to slightly increasing as slopes steepen (Fig. 6c). There is no clear relationship between sea level change (H_s) and L_d (Fig. 6d), which is somewhat surprising given that river mouths and deltas have statistically different mean and median H_s values (Table 2).

To quantify the relative importance of the environmental variables for delta formation, we develop an empirically derived logistic regression. The result of a logistic regression is a statistical model that predicts a dichotomous outcome (in this case, a river creates a delta, or it does not) based on multiple independent variables. This dataset contains eight total independent variables collected on most rivers: four are upstream variables (Q_w, Q_s, Q_s∕Q_w, A_b) and four are downstream variables (H_w, H_t, S_b, H_s). Of the 5399 rivers in this dataset, 490 of them (9.1 %) have data available for all eight independent variables.

The data meet the assumptions of binary logistic regression because the dependent variable has two mutually exclusive outcomes and the sample size is large (45 samples or more per independent variable). Additional assumptions that the data must meet include having little to no multicollinearity and no outliers. We tested for multicollinearity by calculating the Pearson correlation coefficients (R) between all continuous independent variables, and no variables exhibited R>0.9. We also remove 13 rivers that have outliers in any of the independent variables based on a modified z score, whereby an absolute-value-modified z score >3.5 is considered an outlier (Iglewicz and Hoaglin, 1993). The final subset of data used for the regression has n=477 rivers (249 rivers without deltas, 228 rivers with deltas). The samples were randomly separated into training (2∕3 of the samples) and validation (1∕3 of the samples) subsets, each of which represented similar distributions of independent and dependent variables. We do this to see how well the logistic regression can predict delta formation on river mouths not used in development of the equation.

The binary logistic regression between the probability that a river will create a delta and the eight environmental variables yields the following log odds relationship:

where π_delta is the probability that a river will form a delta and ranges from 0 (the river is unlikely to form a delta) to 1 (the river is most likely to form a delta). This is different from the L_d values presented earlier in that it is predicted, whereas L_d is measured. Environmental variables with p>0.05 (Q_s∕Q_w, A_b, S_b, and H_s) are not included in the final empirical relationship because any controls these variables exert on delta formation are minimal (e.g., variations in Q_s∕Q_w have no clear relationship with L_d; Fig. 5d) or are related to variations in the other important variables (e.g., A_b influences Q_w and Q_s).

Thus, the combination of environmental variables that comprises the right side of Eq. (1) predicts the log odds that a river will form a delta. When tested using the validation subset, Eq. (1) has a 74 % success rate at predicting delta presence (Fig. 7), wherein π_delta>0.5 is considered a prediction that a delta exists, and π_delta<0.5 is considered a prediction that no delta exists.

Figure 7Scatter plot of measured versus predicted delta formation. Eq. (1) was used to calculate the predicted probability of delta formation, π_delta, using rivers with necessary data available; n=477 (2∕3 of which was used for training and 1∕3 used for validation). To compare predicted values from Eq. (1) to our collected data the binary observation of delta presence or absence was transformed into a continuous variable. To do this we created 20 equal intervals (π_delta=0.05 bin widths) and averaged π_delta values. L_d is calculated for each bin as the number of rivers with deltas divided by the total number of rivers. The dashed line represents a 1:1 relationship.

Download

This empirically derived relationship can be used to calculate the probability that a certain combination of the most important environmental variables will form a delta. For example, using environmental variable values for the Godavari River in the right-hand side (RHS) of Eq. (1) results in RHS=3.93. The probability that the Godavari River should form a delta is ${\mathit{\pi }}_{\mathrm{delta}}=\frac{e^{\mathrm{RHS}}}{\mathrm{1}+e^{\mathrm{RHS}}}=\mathrm{0.98}$. Thus, the environmental variables that conspire to form the Godavari River are very likely to form a delta, which is not surprising given the existence of the large Godavari River delta.

4.1 Which environmental variables most strongly control delta formation?

We have considered the relationships between eight environmental variables and delta formation. However, determining which variables are most dominant is not straightforward. After all, most combinations of environmental variables that exist globally completely suppress delta formation (60 % of the rivers included in this dataset do not have a delta). Our likelihood analysis shows that deltas are more likely to form at river mouths with large water discharge Q_w (Fig. 5a), sediment discharge Q_s (Fig. 5b), and drainage basin area (Fig. 5c), as well as with small significant wave heights H_w (Fig. 6a) and tidal ranges H_t (Fig. 6b). Results suggest that upstream variables exert a primary control. Increasing upstream variables (Q_w, Q_s, A_b) across their value range accounts for the full range of delta likelihood – that is, the smallest Q_w, Q_s, and A_b values have L_d≈0, and the largest Q_w, Q_s, and A_b have L_d≈1 (Fig. 5). Downstream variables seem to be of secondary importance for forming deltas. Increasing the downstream variables (H_w, H_t) decreases the likelihood that a river forms a delta but does not produce the full range of possible L_d values. At the lowest values of H_w and H_t delta likelihood is still 0.5. Furthermore, when we remove H_w and H_t from Eq. (1) the prediction success rate decreases by only 3 %, from 74 % to 71 %.

These controls on delta formation explain the first-order latitudinal variations observed in Figs. 3 and 4. For example, the peaks in water and sediment discharge values from −9 to 30^∘ and 60 to 75^∘ (Fig. 4) likely explain the similarly located peaks in delta formation (Fig. 3). The suppressing effects of waves and tides can also be seen at a global scale. Low delta formation rates from −57 to −27^∘ and 30 to 60^∘ are likely due to large H_w and H_t values in these regions, where Q_w and Q_s are low (Figs. 3, 4). Moreover, the zone from 60 to 75^∘ that has increased Q_w and Q_s values (Fig. 3) also has some of the lowest H_w and H_t values (Fig. 4). Thus, while high Q_w and Q_s values in this region promote delta formation, the decreased H_w and H_t values also allow delta formation to occur.

Downstream bathymetric slope (S_b) displays a complex relationship with delta likelihood. At slopes <0.006, delta likelihood decreases with increasing slope (Fig. 6c). This is likely because, all else being equal, deeper areas should take longer to fill with sediment and they are also less effective at damping incoming waves and tides. Interestingly, for slopes >0.006, delta likelihood increases with steeper slopes, which is more difficult to explain. Based on visual observation, the steeply dipping basins reflect active margins, and the shallowly dipping basin types reflect passive margins, though we did not pursue a more robust confirmation. If these steeper slopes relate to active margins, then larger sediment sizes and higher supply on active margins may explain the different relationship with delta likelihood than that for the shallowly dipping basin types (Audley-Charles et al., 1977; Orton and Reading, 1993; Milliman and Farnsworth, 2011). After all, the supply of coarser sediment to the coast is more easily retained nearshore (Caldwell and Edmonds, 2014), thereby increasing the likelihood of delta formation.

4.2 The roles of rivers, waves, and tides in delta formation

Our data suggest that deltas are fundamentally created by water and sediment discharge, whereas waves, and possibly tides, suppress delta formation. This is consistent with the notion that delta formation is the result of constructive upstream forces set by the river and destructive downstream marine forces (Fisher, 1969, Boyd et al., 1992, Anthony, 2015). This idea, initially proposed by Fisher (1969), provides a different perspective compared to the oft-cited study on delta morphology and formation from Galloway (1975). Galloway's diagram implies that deltaic formation and morphology are the result of the interplay of the river, waves, and tides. In the case of a purely wave-dominated delta, Galloway's diagram would predict a cuspate delta. Instead, our data clearly show that the most wave-dominated delta is no delta at all, consistent with other studies (Nienhuis et al., 2013; Boyd et al.,1992). This suggests to us that the concept of delta formation and morphology might be better cast as a balance between constructive and destructive forces.

If we consider the perspective that delta formation is the result of a balance between constructive and destructive forces, then new questions emerge: how do wave and tidal processes influence the ability of fluvial processes to construct deltas? How stable is the balance between a given set of constructive and destructive forces? Regarding the last question, there are examples of rapid changes in delta morphology through time, which suggests that the balance can be precarious. The Rhône River delta shifted in morphology from channel-network-dominated in the 16th century to its current wave-smoothed shape as floods and sediment loads declined during the Little Ice Age (14th–19th centuries) (Provansal et al., 2015). The Po River delta showed three morphological transitions each time the balance between river and waves changed over the last 4000 years (Anthony et al., 2014). These examples from the past should direct our attention to how the current configuration of deltas might change in the future. We know that anthropogenic climate change is changing wave conditions (Reguero et al., 2019) and humans are drastically changing water discharge and sediment flux to coastal rivers (Syvitski and Milliman, 2007). It is unclear how the coastal deltas of the world will adapt to these changes in boundary conditions. Future work would benefit from linking our empirically derived delta likelihood predictor with metrics of delta morphology to understand when morphological shifts might occur.